


Next: Theorem of Kutta and
Up: Incompressible Aerodynamics
Previous: Incompressible Aerodynamics
This chapter investigates the forces exerted on a stationary obstacle situated in a uniform, high Reynolds number,
subsonic (and, therefore, effectively incompressible--see Section 1.17) wind, on the assumption that
the obstacle is sufficiently streamlined that there
is no appreciable separation of the boundary layer from its back surface.
Such an obstacle is termed an airfoil (or aerofoil). Obviously, airfoil theory is fundamental to the theory of flight.
Further information on this subject can be found in Milne-Thomson 1958.
The flow around an airfoil is essentially irrotational and inviscid
everywhere apart from a thin boundary layer localized to its surface, and a thin wake emitted by its trailing
edge. (See Sections 8.5 and 8.6.)
It follows that, for the flow external to the
boundary layer and wake, we can write
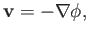 |
(9.1) |
which automatically ensures that the flow is irrotational. Assuming that the flow is also incompressible, so that
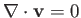 ,
the velocity potential,
,
the velocity potential, 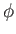 , satisfies Laplace's equation: that is,
, satisfies Laplace's equation: that is,
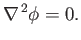 |
(9.2) |
The appropriate boundary condition at the surface of the airfoil is that the normal velocity be zero. In other
words,
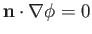 , where
, where 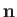 is a unit vector normal to the surface. In general, the
tangential velocity at the airfoil surface, obtained by solving
is a unit vector normal to the surface. In general, the
tangential velocity at the airfoil surface, obtained by solving
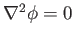 in the external region, subject to the boundary condition
in the external region, subject to the boundary condition
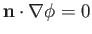 on the surface, is non-zero. Of course, this is inconsistent with the no slip condition, which
demands that the tangential velocity be zero at the surface. (See Section 8.2.)
However, as described in the previous chapter, this inconsistency is resolved by the boundary layer, across which the tangential velocity is
effectively discontinuous, being non-zero on the outer edge of the layer (where it interfaces with the irrotational
flow), and zero on the inner edge (where it interfaces with the airfoil). The discontinuity in the tangential
velocity across the layer implies the presence of bound vortices covering the surface of the airfoil (see Section 9.7), and
also gives rise to a friction drag acting on the airfoil in the direction of the
external flow. However, the magnitude of this drag scales as
on the surface, is non-zero. Of course, this is inconsistent with the no slip condition, which
demands that the tangential velocity be zero at the surface. (See Section 8.2.)
However, as described in the previous chapter, this inconsistency is resolved by the boundary layer, across which the tangential velocity is
effectively discontinuous, being non-zero on the outer edge of the layer (where it interfaces with the irrotational
flow), and zero on the inner edge (where it interfaces with the airfoil). The discontinuity in the tangential
velocity across the layer implies the presence of bound vortices covering the surface of the airfoil (see Section 9.7), and
also gives rise to a friction drag acting on the airfoil in the direction of the
external flow. However, the magnitude of this drag scales as
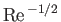 , where
, where 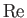 is the Reynolds number of the wind. (See Section 8.5.) Hence, such drag becomes negligibly small in the high Reynolds number limit.
In the following, we shall assume that any form drag, due to the residual separation of the boundary layer at the back of
the airfoil, is also negligibly small. Moreover, for the sake of simplicity, we shall initially restrict our
discussion to two-dimensional situations in which a high Reynolds number wind flows
transversely around a stationary airfoil of infinite length (in the
is the Reynolds number of the wind. (See Section 8.5.) Hence, such drag becomes negligibly small in the high Reynolds number limit.
In the following, we shall assume that any form drag, due to the residual separation of the boundary layer at the back of
the airfoil, is also negligibly small. Moreover, for the sake of simplicity, we shall initially restrict our
discussion to two-dimensional situations in which a high Reynolds number wind flows
transversely around a stationary airfoil of infinite length (in the  -direction) and uniform cross-section (parallel to the
-direction) and uniform cross-section (parallel to the  -
- plane).
plane).



Next: Theorem of Kutta and
Up: Incompressible Aerodynamics
Previous: Incompressible Aerodynamics
Richard Fitzpatrick
2016-03-31