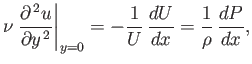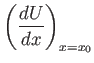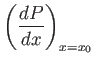Next: Approximate Solutions of Boundary
Up: Incompressible Boundary Layers
Previous: Boundary Layer Separation
Criterion for Boundary Layer Separation
As we have seen, the boundary layer equations (8.110)-(8.113) generally lead to the conclusion that the tangential velocity in a thin boundary layer, 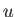 ,
is large compared with the normal velocity,
,
is large compared with the normal velocity, 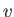 . Mathematically speaking, this result holds everywhere except in the
immediate vicinity of singular points. But, if
. Mathematically speaking, this result holds everywhere except in the
immediate vicinity of singular points. But, if 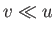 then it follows that the fluid moves predominately parallel to the surface
of the obstacle, and can only move away from this surface to a very limited extent. This restriction effectively precludes separation of the flow from the surface. Hence, we conclude
that separation can only occur at a point at which the solution of the boundary layer
equations is singular.
then it follows that the fluid moves predominately parallel to the surface
of the obstacle, and can only move away from this surface to a very limited extent. This restriction effectively precludes separation of the flow from the surface. Hence, we conclude
that separation can only occur at a point at which the solution of the boundary layer
equations is singular.
As we approach a separation point, we expect the flow to deviate from the boundary layer
towards the interior of the fluid. In other words, we expect the normal velocity to become comparable with the
tangential velocity. However, we have seen that the ratio 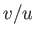 is of order
is of order
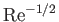 . [See Equation (8.18).] Hence, an increase of
. [See Equation (8.18).] Hence, an increase of 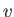 to
such a degree that
to
such a degree that 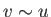 implies an increase by a factor
implies an increase by a factor
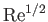 . For sufficiently large Reynolds
numbers, we may suppose that
. For sufficiently large Reynolds
numbers, we may suppose that 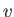 effectively increases by an infinite factor. Indeed, if we employ the dimensionless form of the
boundary layer equations, (8.23)-(8.27), the situation just described is formally
equivalent to an infinite value of the dimensionless normal velocity,
effectively increases by an infinite factor. Indeed, if we employ the dimensionless form of the
boundary layer equations, (8.23)-(8.27), the situation just described is formally
equivalent to an infinite value of the dimensionless normal velocity, 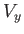 , at the separation point.
, at the separation point.
Let the separation point lie at 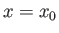 , and let
, and let 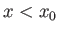 correspond to the region of the boundary layer upstream
of this point. According to the previous discussion,
correspond to the region of the boundary layer upstream
of this point. According to the previous discussion,
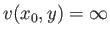 |
(8.121) |
at all  (except, of course,
(except, of course, 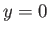 , where the boundary conditions at the surface of the obstacle require that
, where the boundary conditions at the surface of the obstacle require that  ).
It follows that the deriviative
).
It follows that the deriviative
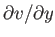 is also infinite at
is also infinite at 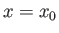 . Hence, the
equation of continuity,
. Hence, the
equation of continuity,
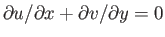 , implies that
, implies that
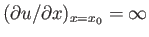 ,
or
,
or
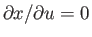 , if
, if  is regarded as a function of
is regarded as a function of 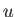 and
and  . Let
. Let
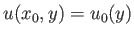 .
Close to the point of separation,
.
Close to the point of separation, 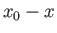 and
and 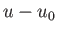 are small. Thus, we can expand
are small. Thus, we can expand 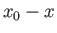 in powers
of
in powers
of 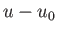 (at fixed
(at fixed  ). Because
). Because
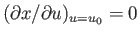 , the first term in this expansion
vanishes identically, and we are left with
, the first term in this expansion
vanishes identically, and we are left with
![$\displaystyle x_0-x = f(y)\,(u-u_0)^2 + {\cal O}\left[(u-u_0)^3\right],$](img3115.png) |
(8.122) |
or
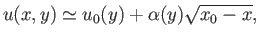 |
(8.123) |
where
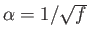 is some function of
is some function of  . From the equation of continuity,
. From the equation of continuity,
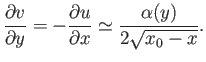 |
(8.124) |
Upon integration, the previous expression yields
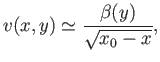 |
(8.125) |
where
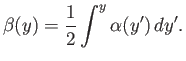 |
(8.126) |
The equation of tangential motion in the boundary layer, (8.111), is written
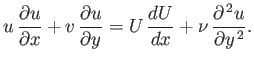 |
(8.127) |
As is clear from Equation (8.123), the derivative
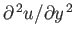 does not become
infinite as
does not become
infinite as
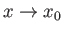 . The same is true of the function
. The same is true of the function 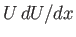 , which is determined from the
flow outside the boundary layer. However, both terms on the left-hand side of the previous expression become
infinite as
, which is determined from the
flow outside the boundary layer. However, both terms on the left-hand side of the previous expression become
infinite as
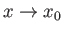 . Hence, in the immediate vicinity of the separation point,
. Hence, in the immediate vicinity of the separation point,
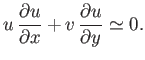 |
(8.128) |
Because
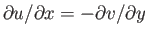 , we can rewrite this equation in the form
, we can rewrite this equation in the form
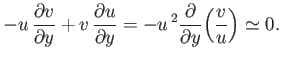 |
(8.129) |
Because 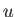 does not, in general, vanish at
does not, in general, vanish at 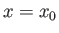 , we conclude that
, we conclude that
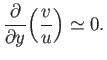 |
(8.130) |
In other words, 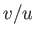 is a function of
is a function of  only. From Equations (8.123) and (8.125),
only. From Equations (8.123) and (8.125),
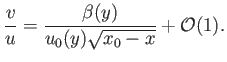 |
(8.131) |
Hence, if this ratio is a function of  alone then
alone then
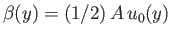 , where
, where 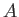 is a constant: that is,
is a constant: that is,
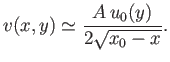 |
(8.132) |
Finally, because Equation (8.126) yields
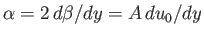 , we obtain
, we obtain
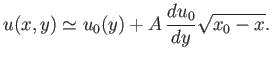 |
(8.133) |
The previous two expressions specify 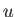 and
and 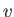 as functions of
as functions of  and
and  near the point of separation. Beyond the point of separation, that is
for
near the point of separation. Beyond the point of separation, that is
for 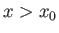 , the expressions are physically meaningless, because the
square roots become imaginary. This implies that the solutions of the
boundary layer equations cannot sensibly be continued beyond the separation
point.
, the expressions are physically meaningless, because the
square roots become imaginary. This implies that the solutions of the
boundary layer equations cannot sensibly be continued beyond the separation
point.
The standard boundary conditions at the surface of the obstacle require
that 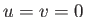 at
at 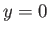 . It, therefore, follows from Equations (8.132) and (8.133) that
. It, therefore, follows from Equations (8.132) and (8.133) that
Thus, we obtain the important prediction that both the
tangential velocity, 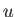 , and its first derivative,
, and its first derivative,
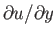 , are zero at the separation point (i.e.,
, are zero at the separation point (i.e., 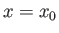 and
and 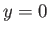 ). This result was originally
obtained by Prandtl, although the argument we have used to derive it is due to L.D. Landau (1908-1968) (Landau and Lifshitz 1987).
). This result was originally
obtained by Prandtl, although the argument we have used to derive it is due to L.D. Landau (1908-1968) (Landau and Lifshitz 1987).
If the constant 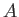 in expressions (8.132) and (8.133) happens to be
zero then the point
in expressions (8.132) and (8.133) happens to be
zero then the point 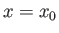 and
and 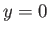 , at which the derivative
, at which the derivative
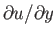 vanishes,
has no particular properties, and is not a point of separation. However, there is no reason, in
general, why
vanishes,
has no particular properties, and is not a point of separation. However, there is no reason, in
general, why 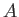 should take the special value zero. Thus, in practice, a point on the surface
of an obstacle at which
should take the special value zero. Thus, in practice, a point on the surface
of an obstacle at which
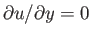 is always a point of separation.
is always a point of separation.
Incidentally, if there were no separation at the point 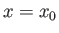 (i.e., if
(i.e., if  ) then we
would have
) then we
would have
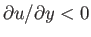 for
for 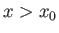 . In other words,
. In other words, 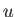 would become negative as we move
away from the surface,
would become negative as we move
away from the surface,  being still small. That is, the fluid beyond the point
being still small. That is, the fluid beyond the point 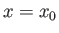 would move tangentially, in the region of the boundary layer immediately adjacent to the surface, in the
direction opposite to that of the external flow: that is, there would be ``back-flow'' in this region.
In practice, the flow separates from the surface at
would move tangentially, in the region of the boundary layer immediately adjacent to the surface, in the
direction opposite to that of the external flow: that is, there would be ``back-flow'' in this region.
In practice, the flow separates from the surface at 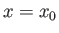 , and the back-flow migrates into the wake.
, and the back-flow migrates into the wake.
The dimensionless boundary layer equations, (8.23)-(8.27), are independent of the Reynolds
number of the external flow (assuming that this number is much greater than unity). Thus, it follows
that the point on the surface of the obstacle at which
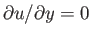 is also independent of the
Reynolds number. In other words, the location of the separation point is independent of the Reynolds
number (as long as this number is large, and the flow in the boundary layer is non-turbulent).
is also independent of the
Reynolds number. In other words, the location of the separation point is independent of the Reynolds
number (as long as this number is large, and the flow in the boundary layer is non-turbulent).
At 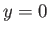 , the equation of tangential motion in the boundary layer, (8.111),
is written
, the equation of tangential motion in the boundary layer, (8.111),
is written
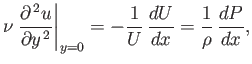 |
(8.136) |
where 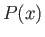 is the pressure just outside the layer, and use has been made of Equation (8.6). Because
is the pressure just outside the layer, and use has been made of Equation (8.6). Because 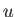 is positive, and increases away from the surface (upstream of the separation point), it follows that
is positive, and increases away from the surface (upstream of the separation point), it follows that
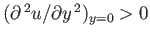 at the separation point itself, where
at the separation point itself, where
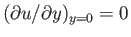 . Hence, according to the previous equation,
. Hence, according to the previous equation,
In other words, we predict that the external tangential flow is always decelerating at the separation point, whereas the pressure gradient is always
adverse (i.e., such as to decelerate the tangential flow), in agreement with experimental observations.



Next: Approximate Solutions of Boundary
Up: Incompressible Boundary Layers
Previous: Boundary Layer Separation
Richard Fitzpatrick
2016-03-31
![]() is of order
is of order
![]() . [See Equation (8.18).] Hence, an increase of
. [See Equation (8.18).] Hence, an increase of ![]() to
such a degree that
to
such a degree that ![]() implies an increase by a factor
implies an increase by a factor
![]() . For sufficiently large Reynolds
numbers, we may suppose that
. For sufficiently large Reynolds
numbers, we may suppose that ![]() effectively increases by an infinite factor. Indeed, if we employ the dimensionless form of the
boundary layer equations, (8.23)-(8.27), the situation just described is formally
equivalent to an infinite value of the dimensionless normal velocity,
effectively increases by an infinite factor. Indeed, if we employ the dimensionless form of the
boundary layer equations, (8.23)-(8.27), the situation just described is formally
equivalent to an infinite value of the dimensionless normal velocity, ![]() , at the separation point.
, at the separation point.
![]() , and let
, and let ![]() correspond to the region of the boundary layer upstream
of this point. According to the previous discussion,
correspond to the region of the boundary layer upstream
of this point. According to the previous discussion,
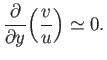
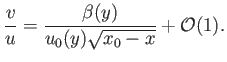
![]() at
at ![]() . It, therefore, follows from Equations (8.132) and (8.133) that
. It, therefore, follows from Equations (8.132) and (8.133) that
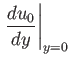
![]() in expressions (8.132) and (8.133) happens to be
zero then the point
in expressions (8.132) and (8.133) happens to be
zero then the point ![]() and
and ![]() , at which the derivative
, at which the derivative
![]() vanishes,
has no particular properties, and is not a point of separation. However, there is no reason, in
general, why
vanishes,
has no particular properties, and is not a point of separation. However, there is no reason, in
general, why ![]() should take the special value zero. Thus, in practice, a point on the surface
of an obstacle at which
should take the special value zero. Thus, in practice, a point on the surface
of an obstacle at which
![]() is always a point of separation.
is always a point of separation.
![]() (i.e., if
(i.e., if ![]() ) then we
would have
) then we
would have
![]() for
for ![]() . In other words,
. In other words, ![]() would become negative as we move
away from the surface,
would become negative as we move
away from the surface, ![]() being still small. That is, the fluid beyond the point
being still small. That is, the fluid beyond the point ![]() would move tangentially, in the region of the boundary layer immediately adjacent to the surface, in the
direction opposite to that of the external flow: that is, there would be ``back-flow'' in this region.
In practice, the flow separates from the surface at
would move tangentially, in the region of the boundary layer immediately adjacent to the surface, in the
direction opposite to that of the external flow: that is, there would be ``back-flow'' in this region.
In practice, the flow separates from the surface at ![]() , and the back-flow migrates into the wake.
, and the back-flow migrates into the wake.
![]() is also independent of the
Reynolds number. In other words, the location of the separation point is independent of the Reynolds
number (as long as this number is large, and the flow in the boundary layer is non-turbulent).
is also independent of the
Reynolds number. In other words, the location of the separation point is independent of the Reynolds
number (as long as this number is large, and the flow in the boundary layer is non-turbulent).
![]() , the equation of tangential motion in the boundary layer, (8.111),
is written
, the equation of tangential motion in the boundary layer, (8.111),
is written