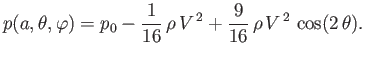Next: Motion of a Submerged
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Dipole Point Sources
Flow Past a Spherical Obstacle
Consider the steady flow pattern produced when an impenetrable rigid
spherical obstacle is placed in a uniformly flowing, incompressible, inviscid fluid.
For instance, suppose that the radius of the sphere is  , and that its center coincides
with the origin. Furthermore, let the unperturbed fluid
velocity be of magnitude
, and that its center coincides
with the origin. Furthermore, let the unperturbed fluid
velocity be of magnitude  , and be directed parallel to the
, and be directed parallel to the  -axis. We expect the
flow pattern to remain unperturbed very far away from the sphere. In other words,
we expect
-axis. We expect the
flow pattern to remain unperturbed very far away from the sphere. In other words,
we expect
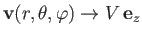 as
as
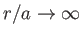 . Given that the fluid velocity field
a large distance upstream of the sphere is irrotational (because a uniform flow pattern is automatically
irrotational), it follows from the Kelvin circulation theorem that the velocity field remains irrotational
as it is convected past the sphere. (See Section 4.14.) Hence, we can write
. Given that the fluid velocity field
a large distance upstream of the sphere is irrotational (because a uniform flow pattern is automatically
irrotational), it follows from the Kelvin circulation theorem that the velocity field remains irrotational
as it is convected past the sphere. (See Section 4.14.) Hence, we can write
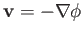 , where
, where
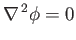 |
(7.45) |
(because
the fluid is incompressible.) The boundary conditions are
and
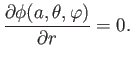 |
(7.47) |
The latter constraint arises because the surface of the sphere is impenetrable, which implies that
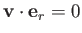 at
at  .
.
Let us search for an axisymmetric solution of Equation (7.45) of the
form
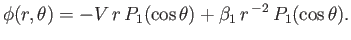 |
(7.48) |
It can be seen, by comparison with Equation (7.23), that the previous expression definitely solves Equation (7.45).
Moreover, the expression also automatically satisfies the boundary condition (7.46) [because
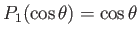 ]. The remaining boundary condition, (7.47), yields
]. The remaining boundary condition, (7.47), yields
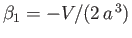 . Hence, we obtain
. Hence, we obtain
![$\displaystyle \phi(r,\theta) = - V\,a\left[\frac{r}{a}+\frac{1}{2}\left(\frac{a}{r}\right)^2\right]\cos\theta,$](img2645.png) |
(7.49) |
or
Because the solutions of Laplace's equation, subject to well-posed boundary conditions, are unique (Riley 1974),
we can be sure that the previous axisymmetric solution is the most general solution to the problem.
It is clear, by comparison with Equations (7.28) and (7.42), that the velocity potential
(7.49) is the superposition of that associated with uniform flow with velocity  , parallel
to the
, parallel
to the  -axis, and a dipole point source of strength
-axis, and a dipole point source of strength
 , located at the origin. Thus,
making use of Equations (7.26) and (7.44), the associated stream function takes the
form
, located at the origin. Thus,
making use of Equations (7.26) and (7.44), the associated stream function takes the
form
![$\displaystyle \psi = -\frac{1}{2}\,V\,r^{\,2}\,\sin^2\theta\left(1-\frac{a^{\,3...
...2}\,V\,\varpi^{\,2}\left[1-\frac{a^{\,3}}{(\varpi^{\,2}+z^{\,2})^{3/2}}\right].$](img2649.png) |
(7.52) |
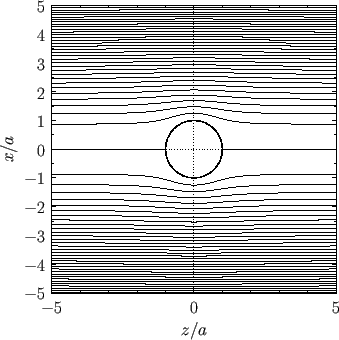
Figure 7.4 show the contours of this stream function.
Figure:
Contours of the stream function generated by a spherical obstacle of radius  placed in the uniform flow field
placed in the uniform flow field
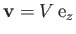 .
.
 |
Bernoulli's theorem yields (see Section 4.3)
 |
(7.53) |
where  is the uniform fluid mass density, and
is the uniform fluid mass density, and 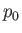 the fluid pressure at infinity. Thus, making use of Equations (7.50) and (7.51), the
pressure distribution on the surface of the sphere can be written
the fluid pressure at infinity. Thus, making use of Equations (7.50) and (7.51), the
pressure distribution on the surface of the sphere can be written
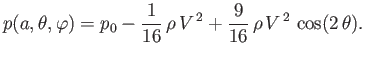 |
(7.54) |
The net force exerted on the sphere by the fluid has the Cartesian components
where the integrals are over all solid angle. Thus, it follows that
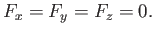 |
(7.58) |
In other words, the fluid exerts zero net force on the sphere, in accordance with d'Alembert's paradox. (See Section 4.5.)



Next: Motion of a Submerged
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Dipole Point Sources
Richard Fitzpatrick
2016-03-31
![]() , parallel
to the
, parallel
to the ![]() -axis, and a dipole point source of strength
-axis, and a dipole point source of strength
![]() , located at the origin. Thus,
making use of Equations (7.26) and (7.44), the associated stream function takes the
form
, located at the origin. Thus,
making use of Equations (7.26) and (7.44), the associated stream function takes the
form
![$\displaystyle \psi = -\frac{1}{2}\,V\,r^{\,2}\,\sin^2\theta\left(1-\frac{a^{\,3...
...2}\,V\,\varpi^{\,2}\left[1-\frac{a^{\,3}}{(\varpi^{\,2}+z^{\,2})^{3/2}}\right].$](img2649.png)