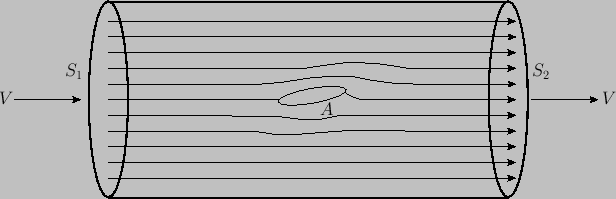
 |
Consider two cross-sections, ![]() and
and ![]() , a great distance upstream and downstream of
, a great distance upstream and downstream of ![]() , respectively.
The fluid between these sections can be split into a great many stream filaments to each of which Euler's
momentum theorem is applicable. The outer filaments are bounded by the walls of the tube, and so the thrust components
acting on these are directed perpendicular to the flow. The walls of the filaments in contact with
, respectively.
The fluid between these sections can be split into a great many stream filaments to each of which Euler's
momentum theorem is applicable. The outer filaments are bounded by the walls of the tube, and so the thrust components
acting on these are directed perpendicular to the flow. The walls of the filaments in contact with ![]() are acted on by
the obstacle, which exerts on them a force whose component in the direction of the flow is
are acted on by
the obstacle, which exerts on them a force whose component in the direction of the flow is ![]() . By Euler's
theorem, the resultant of all of the thrusts acting on the fluid in the tube is
. By Euler's
theorem, the resultant of all of the thrusts acting on the fluid in the tube is
| (4.11) |
By Bernoulli's theorem, the pressure ![]() acting across
acting across ![]() is the same as the pressure
is the same as the pressure ![]() acting
across
acting
across ![]() . Thus, according to Euler's theorem,
. Thus, according to Euler's theorem,
| (4.12) |
| (4.13) |
If we suppose the walls of the tube to recede to infinity then we obtain the case of an obstacle immersed in a moving stream
that is unbounded in every direction. The previous proof still shows that ![]() .
.
Finally, if we impose on the whole system a uniform velocity ![]() in the direction opposite to that of the stream then
the fluid at a great distance is reduced to rest, and the obstacle
in the direction opposite to that of the stream then
the fluid at a great distance is reduced to rest, and the obstacle ![]() moves with the uniform speed
moves with the uniform speed ![]() . However, superposing
a uniform flow does not alter the dynamical conditions. Therefore, we conclude that the resistance to a
solid body moving with uniform velocity through an unbounded inviscid fluid, otherwise at rest, is zero.
. However, superposing
a uniform flow does not alter the dynamical conditions. Therefore, we conclude that the resistance to a
solid body moving with uniform velocity through an unbounded inviscid fluid, otherwise at rest, is zero.