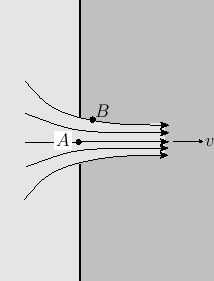
 |
Let ![]() be the cross-sectional area of the orifice, and
be the cross-sectional area of the orifice, and
![]() that of the vena contracta. Here,
that of the vena contracta. Here, ![]() is known as the contraction coefficient. Let us apply Bernoulli's theorem to a streamline that
starts on the surface of the fluid within the container, and ends in the vena contracta. Suppose that the
surface of the fluid lies a height
is known as the contraction coefficient. Let us apply Bernoulli's theorem to a streamline that
starts on the surface of the fluid within the container, and ends in the vena contracta. Suppose that the
surface of the fluid lies a height ![]() above the orifice. Let us assume that the fluid close to the surface is
essentially at rest (which implies that the outflow through the orifice is not sufficiently strong to cause the surface level
to drop at a significant rate.) Let
above the orifice. Let us assume that the fluid close to the surface is
essentially at rest (which implies that the outflow through the orifice is not sufficiently strong to cause the surface level
to drop at a significant rate.) Let ![]() be the uniform fluid velocity in the vena contracta.
Of course, the pressure is atmospheric both at the surface of the fluid and in the vena contracta. It
follows that
be the uniform fluid velocity in the vena contracta.
Of course, the pressure is atmospheric both at the surface of the fluid and in the vena contracta. It
follows that
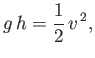 |
(4.14) |
| (4.16) |
Let
![]() be the hydrostatic pressure at the level of the orifice when the orifice is closed. Here,
be the hydrostatic pressure at the level of the orifice when the orifice is closed. Here, ![]() is
atmospheric pressure. The fluid experiences a
thrust
is
atmospheric pressure. The fluid experiences a
thrust ![]() from the section of the wall directly opposite the orifice, and a thrust
from the section of the wall directly opposite the orifice, and a thrust ![]() from the
section of the wall closing the orifice. Let us suppose, as a first approximation, that the
hydrostatic pressure remains unaltered when the orifice is opened. In this situation, the fluid
experiences a thrust
from the
section of the wall closing the orifice. Let us suppose, as a first approximation, that the
hydrostatic pressure remains unaltered when the orifice is opened. In this situation, the fluid
experiences a thrust ![]() from the section of the wall directly opposite the orifice, and a thrust
from the section of the wall directly opposite the orifice, and a thrust
![]() from the orifice. The net thrust,
from the orifice. The net thrust,
![]() , is responsible for accelerating the jet.
Now, the jet's rate of momentum outflow is
, is responsible for accelerating the jet.
Now, the jet's rate of momentum outflow is
![]() . Momentum conservation yields
. Momentum conservation yields
| (4.17) |
In reality, Bernoulli's theorem suggests that when the orifice is opened the pressure on the walls
in the neighborhood of the orifice will fall below the hydrostatic value, which implies that the
accelerating thrust is actually greater than
![]() . Consequently,
. Consequently,
![]() . Obviously,
. Obviously, ![]() cannot exceed unity, so we conclude that, in general,
cannot exceed unity, so we conclude that, in general,
![]() . For instance,
if the orifice is a circular hole punched in a thin plate then the contraction coefficient is observed to take the
value
. For instance,
if the orifice is a circular hole punched in a thin plate then the contraction coefficient is observed to take the
value ![]() (Batchelor 2000).
(Batchelor 2000).
Suppose, however, that we fit a small cylindrical nozzle projecting inward from the orifice, as shown in Figure 4.4.
In this case, the original assumption that the pressure
on the walls in the neighborhood of the orifice is hydrostatic is essentially correct. This follows because the region where
the lines of flow are converging on the orifice is far removed from the walls, and the velocity of the fluid in contact with
the walls is negligible. Thus, the contraction coefficient is exactly ![]() . This arrangement is
known as a Borda mouthpiece, after Jean-Charles Borda (1733-1799).
. This arrangement is
known as a Borda mouthpiece, after Jean-Charles Borda (1733-1799).