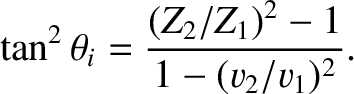-
- Show that the one-dimensional plane wave, (7.1), is a solution of the one-dimensional wave equation, (7.8),
provided that
- Demonstrate that the three-dimensional plane wave, (7.5), is a solution of the three-dimensional wave
equation, (7.9), as long as
-
- Demonstrate that for a cylindrically symmetric wavefunction
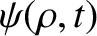 , where
, where
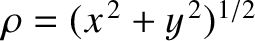 , the
three-dimensional wave equation (7.9)
can be rewritten
, the
three-dimensional wave equation (7.9)
can be rewritten
- Show that
is an approximate solution of this equation in the limit
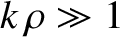 , where
, where
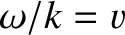 .
.
-
- Demonstrate that for a spherically symmetric wavefunction
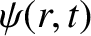 , where
, where
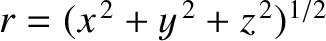 , the
three-dimensional wave equation (7.9)
can be rewritten
, the
three-dimensional wave equation (7.9)
can be rewritten
- Show that
is a solution of this equation, where
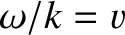 .
.
- Consider an elastic sheet stretched over a rectangular frame that extends from
 to
to  , and from
, and from 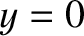 to
to 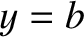 .
Suppose that
Show that the amplitudes and phase angles in the normal mode expansion (7.28) are given by
where
.
Suppose that
Show that the amplitudes and phase angles in the normal mode expansion (7.28) are given by
where
- The radial oscillations of an ideal gas in a spherical cavity of radius
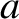 are governed by the
spherical wave equation
are governed by the
spherical wave equation
subject to the boundary condition
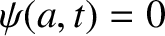 .
Here,
.
Here,
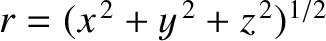 is a spherical coordinate,
is a spherical coordinate, 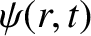 is the radial displacement, and
is the radial displacement, and  is the speed of sound. Show that the general
solution of this equation is written
is the speed of sound. Show that the general
solution of this equation is written
where
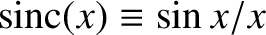 ,
,
and 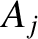 ,
, 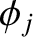 are arbitrary constants.
are arbitrary constants.
- Show that a light-ray entering a planar transparent plate of thickness
 and refractive index
and refractive index  emerges parallel to
its original direction. Show that the lateral displacement of the ray is
emerges parallel to
its original direction. Show that the lateral displacement of the ray is
where 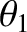 and
and 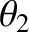 are the angles of incidence and refraction, respectively, at the front side of the plate.
are the angles of incidence and refraction, respectively, at the front side of the plate.
- Suppose that a light-ray is incident on the front (air/glass) interface of a uniform pane
of glass of refractive index
 at the Brewster angle. Demonstrate that the refracted ray
is also incident on the rear (glass/air) interface of the pane at the Brewster
angle. [From Fitzpatrick 2008.]
at the Brewster angle. Demonstrate that the refracted ray
is also incident on the rear (glass/air) interface of the pane at the Brewster
angle. [From Fitzpatrick 2008.]
- Show that the Fresnel relations, (7.75) and (7.76), for the polarization in which the magnetic intensities of all three waves are
parallel to the interface can be written
where
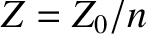 represents impedance. (Here,
represents impedance. (Here, 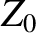 is the impedance of free space, and
is the impedance of free space, and  the refractive index.)
the refractive index.)
- Demonstrate that the Fresnel relations, (7.97) and (7.98), for the other polarization take the form
- Show that the expressions, (7.222) and (7.223), for the coefficients of reflection and transmission for a sound wave obliquely incident at
an interface between two immiscible fluids can be written
where
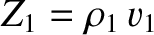 and
and
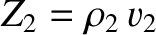 are the acoustic impedances of the two fluids.
are the acoustic impedances of the two fluids.
- Show that the expression, (7.224), for the angle of intromission can be written
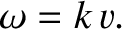
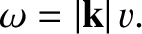
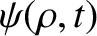 , where
, where
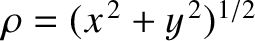 , the
three-dimensional wave equation (7.9)
can be rewritten
, the
three-dimensional wave equation (7.9)
can be rewritten
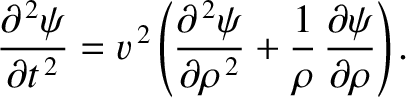
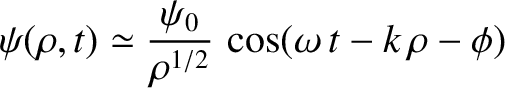
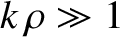 , where
, where
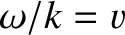 .
.
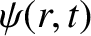 , where
, where
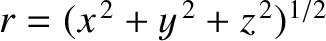 , the
three-dimensional wave equation (7.9)
can be rewritten
, the
three-dimensional wave equation (7.9)
can be rewritten
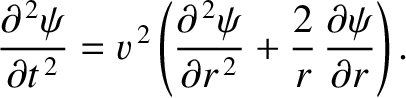
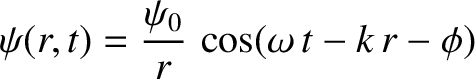
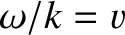 .
.
 to
to  , and from
, and from 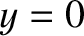 to
to 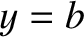 .
Suppose that
.
Suppose that
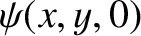
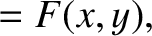
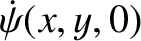
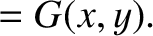
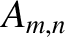

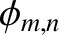
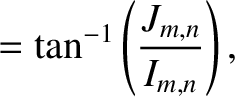
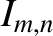
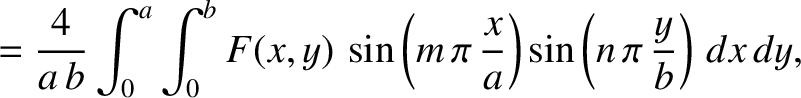
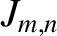
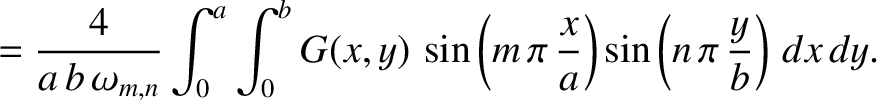
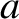 are governed by the
spherical wave equation
are governed by the
spherical wave equation
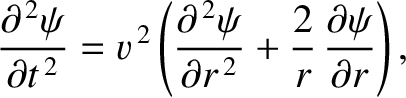
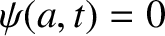 .
Here,
.
Here,
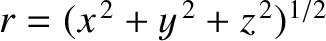 is a spherical coordinate,
is a spherical coordinate, 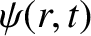 is the radial displacement, and
is the radial displacement, and  is the speed of sound. Show that the general
solution of this equation is written
is the speed of sound. Show that the general
solution of this equation is written
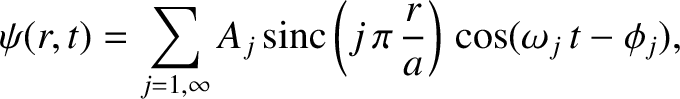
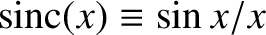 ,
,
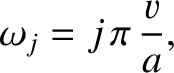
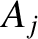 ,
, 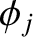 are arbitrary constants.
are arbitrary constants.
 and refractive index
and refractive index  emerges parallel to
its original direction. Show that the lateral displacement of the ray is
emerges parallel to
its original direction. Show that the lateral displacement of the ray is
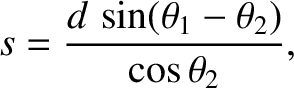
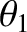 and
and 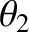 are the angles of incidence and refraction, respectively, at the front side of the plate.
are the angles of incidence and refraction, respectively, at the front side of the plate.
 at the Brewster angle. Demonstrate that the refracted ray
is also incident on the rear (glass/air) interface of the pane at the Brewster
angle. [From Fitzpatrick 2008.]
at the Brewster angle. Demonstrate that the refracted ray
is also incident on the rear (glass/air) interface of the pane at the Brewster
angle. [From Fitzpatrick 2008.]
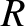
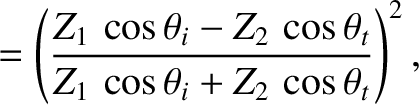
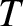
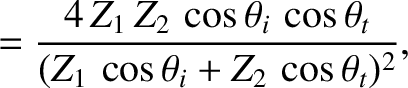
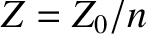 represents impedance. (Here,
represents impedance. (Here, 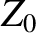 is the impedance of free space, and
is the impedance of free space, and  the refractive index.)
the refractive index.)
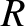
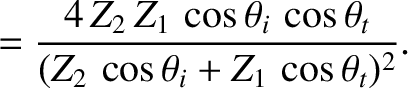
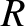
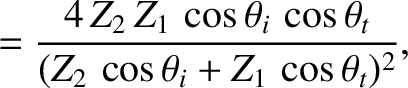
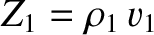 and
and
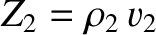 are the acoustic impedances of the two fluids.
are the acoustic impedances of the two fluids.