Next: Three-Dimensional Wave Equation Up: Multi-Dimensional Waves Previous: Introduction Contents
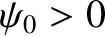 , wavenumber
, wavenumber 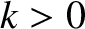 , and angular frequency
, and angular frequency 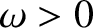 ,
propagating in the positive
,
propagating in the positive  -direction, can be represented in terms of a wavefunction of the form
This type of wave is conventionally termed a one-dimensional plane wave. It is one-dimensional
because its associated wavefunction only depends on a single Cartesian coordinate.
Furthermore, it is a plane wave because the wave maxima, which are located at
where
-direction, can be represented in terms of a wavefunction of the form
This type of wave is conventionally termed a one-dimensional plane wave. It is one-dimensional
because its associated wavefunction only depends on a single Cartesian coordinate.
Furthermore, it is a plane wave because the wave maxima, which are located at
where  is an integer, consist of a series of parallel planes, normal to the
is an integer, consist of a series of parallel planes, normal to the  -axis, that are equally spaced a distance
-axis, that are equally spaced a distance
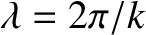 apart, and propagate along the
apart, and propagate along the
 -axis at the fixed phase velocity
-axis at the fixed phase velocity
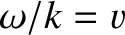 , where
, where  is the characteristic wave speed.
These conclusions follow because Equation (7.2) can be rewritten in the form
where
is the characteristic wave speed.
These conclusions follow because Equation (7.2) can be rewritten in the form
where
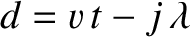 . Moreover, Equation (7.3)
is the equation of a plane, normal to the
. Moreover, Equation (7.3)
is the equation of a plane, normal to the  -axis, whose distance of closest approach to the
origin is
-axis, whose distance of closest approach to the
origin is  .
.
The previous equation can also be written in the coordinate-free form
where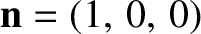 is a unit
vector directed along the
is a unit
vector directed along the  -axis, and
-axis, and
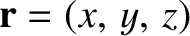 represents the vector displacement of a general point from the origin. Because there is nothing special about the
represents the vector displacement of a general point from the origin. Because there is nothing special about the  -direction, it follows that if
-direction, it follows that if 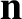 is re-interpreted as a
unit vector pointing in an arbitrary direction then Equation (7.4) can be re-interpreted as the general equation of a plane (Fitzpatrick 2008).
As before, the plane is normal to
is re-interpreted as a
unit vector pointing in an arbitrary direction then Equation (7.4) can be re-interpreted as the general equation of a plane (Fitzpatrick 2008).
As before, the plane is normal to
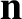 , and its distance of closest approach to the origin is
, and its distance of closest approach to the origin is  . See Figure 7.1. This observation allows us to write the three-dimensional
equivalent to the wavefunction (7.1) as
where the constant vector
. See Figure 7.1. This observation allows us to write the three-dimensional
equivalent to the wavefunction (7.1) as
where the constant vector
 is known as the wavevector. The wave represented in the previous expression is conventionally termed
a three-dimensional plane wave. It is three-dimensional because its wavefunction,
is known as the wavevector. The wave represented in the previous expression is conventionally termed
a three-dimensional plane wave. It is three-dimensional because its wavefunction,
 , depends on all
three Cartesian coordinates. Moreover, it is a plane wave because the wave maxima are located at
, depends on all
three Cartesian coordinates. Moreover, it is a plane wave because the wave maxima are located at
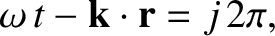 |
(7.6) |
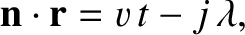 |
(7.7) |
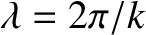 , and
, and
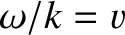 . The wavenumber,
. The wavenumber,  , is the
magnitude of the wavevector,
, is the
magnitude of the wavevector, 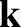 ; that is,
; that is,
 .
It follows, by comparison with Equation (7.4), that the
wave maxima consist of a series of parallel planes, normal to the wavevector, that are equally spaced a distance
.
It follows, by comparison with Equation (7.4), that the
wave maxima consist of a series of parallel planes, normal to the wavevector, that are equally spaced a distance  apart, and propagate in the
apart, and propagate in the 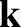 -direction at the fixed phase velocity
-direction at the fixed phase velocity
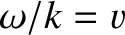 . See Figure 7.2. Hence, the direction of the wavevector corresponds to the direction of wave propagation.
The most general expression for the wavefunction of a three-dimensional plane wave is
. See Figure 7.2. Hence, the direction of the wavevector corresponds to the direction of wave propagation.
The most general expression for the wavefunction of a three-dimensional plane wave is
 , where
, where
 is a constant phase angle. As is readily demonstrated, the inclusion of a non-zero phase angle in the wavefunction
shifts all the wave maxima a distance
is a constant phase angle. As is readily demonstrated, the inclusion of a non-zero phase angle in the wavefunction
shifts all the wave maxima a distance
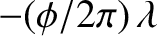 in the
in the 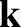 -direction. In the following, whenever possible,
-direction. In the following, whenever possible,  is
set to zero, for the sake of simplicity.
is
set to zero, for the sake of simplicity.