Traveling Waves in Infinite Continuous Medium
Consider solutions of the wave equation, (6.1), in an infinite medium. Such a medium does not possess any spatial boundaries, and so is not
subject to boundary constraints. Hence, there is no particular reason why a
wave of definite wavelength should have stationary nodes or anti-nodes. In other
words, Equation (6.2) may not be the only permissible type of wave solution in an
infinite medium. What other kind of solution could we have? Suppose that
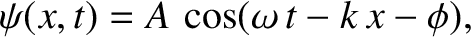 |
(6.7) |
where 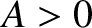 ,
, 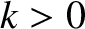 ,
, 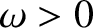 , and
, and  are constants. This solution is interpreted as a wave of amplitude
are constants. This solution is interpreted as a wave of amplitude 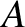 , wavenumber
, wavenumber  , wavelength
, wavelength
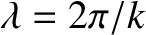 , angular frequency
, angular frequency  , frequency (in hertz)
, frequency (in hertz)
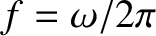 , period
, period 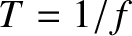 , and phase angle
, and phase angle  . It can be seen that
. It can be seen that
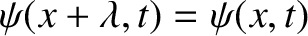 , and
, and
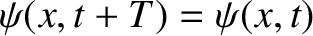 ,
for all
,
for all  and
and  . In other words, the wave is periodic in space with period
. In other words, the wave is periodic in space with period  ,
and periodic in time with period
,
and periodic in time with period  . A wave maximum corresponds to
a point at which
. A wave maximum corresponds to
a point at which
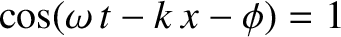 . It follows, from the well-known
properties of the cosine function, that the various wave maxima are located at
. It follows, from the well-known
properties of the cosine function, that the various wave maxima are located at
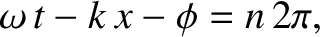 |
(6.8) |
where  is an integer. Differentiating the previous expression with respect to
is an integer. Differentiating the previous expression with respect to  ,
and rearranging, the equation of motion of a particular maximum becomes
,
and rearranging, the equation of motion of a particular maximum becomes
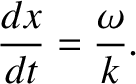 |
(6.9) |
We conclude that the wave maximum in question propagates along the  -axis at the
velocity
-axis at the
velocity
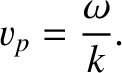 |
(6.10) |
It can be shown that the other wave maxima (as well as the wave minima and the wave zeros) also propagate
along the  -axis at the same velocity. In fact, the whole wave pattern
propagates in the positive
-axis at the same velocity. In fact, the whole wave pattern
propagates in the positive  -direction without changing shape. The characteristic propagation velocity
-direction without changing shape. The characteristic propagation velocity 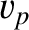 is known as the phase velocity, because
it is the velocity of constant phase points on the wave disturbance (i.e., points that satisfy
is known as the phase velocity, because
it is the velocity of constant phase points on the wave disturbance (i.e., points that satisfy
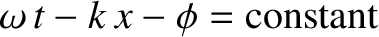 ). For obvious reasons, the type of wave solution specified in Equation (6.7) is called a traveling
wave.
). For obvious reasons, the type of wave solution specified in Equation (6.7) is called a traveling
wave.
Substitution of Equation (6.7) into the wave equation, (6.1), yields the familiar dispersion relation
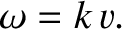 |
(6.11) |
We conclude that the traveling wave solution (6.7) satisfies the wave equation
provided
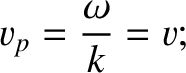 |
(6.12) |
that is, provided the phase velocity of the wave takes the fixed value  .
It follows that the constant
.
It follows that the constant 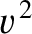 , that appears in the wave
equation, (6.1), can be interpreted as the square of the velocity with which traveling waves propagate through the
medium in question. Hence, from the discussions in Sections 4.3, 5.2, and 5.3, transverse waves propagate along strings of tension
, that appears in the wave
equation, (6.1), can be interpreted as the square of the velocity with which traveling waves propagate through the
medium in question. Hence, from the discussions in Sections 4.3, 5.2, and 5.3, transverse waves propagate along strings of tension  and
mass per unit length
and
mass per unit length  at the phase velocity
at the phase velocity
 , longitudinal
waves propagate along thin elastic rods of Young's modulus
, longitudinal
waves propagate along thin elastic rods of Young's modulus 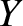 and mass density
and mass density
 at the phase velocity
at the phase velocity
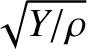 , and sound waves propagate
through ideal gases of pressure
, and sound waves propagate
through ideal gases of pressure 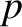 , mass density
, mass density  , and ratio of specific heats
, and ratio of specific heats  , at the phase velocity
, at the phase velocity
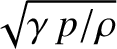 .
.
Table: 6.1
Calculated and measured longitudinal wave speeds in thin rods made up of common metals. Sources: Haynes and Lide 2011c, Wikipedia contributors 2018.
| Metal |
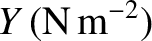 |
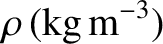 |
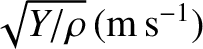 |
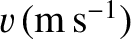 |
| |
|
|
|
|
| Aluminum |
 |
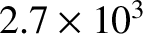 |
 |
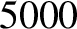 |
| Nickel |
 |
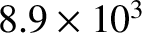 |
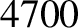 |
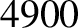 |
| Zinc |
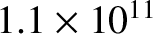 |
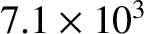 |
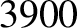 |
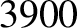 |
| Copper |
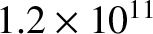 |
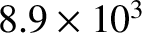 |
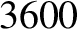 |
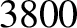 |
| Silver |
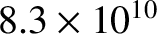 |
 |
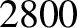 |
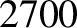 |
| Tin |
 |
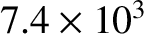 |
 |
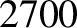 |
| Lead |
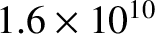 |
 |
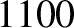 |
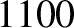 |
|
Table 6.1 displays
calculated and measured longitudinal wave speeds in thin rods made up of various common metals. It can
be seen that the agreement between the two is excellent.
An ideal gas of mass  and molecular weight
and molecular weight  satisfies the
ideal gas equation of state,
satisfies the
ideal gas equation of state,
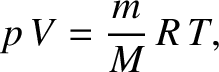 |
(6.13) |
where 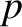 is the pressure,
is the pressure, 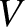 the volume,
the volume,
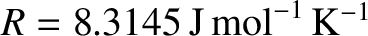 the molar ideal gas constant, and
the molar ideal gas constant, and  the
absolute temperature (Reif 2008). Because the ratio
the
absolute temperature (Reif 2008). Because the ratio 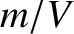 is equal to the density,
is equal to the density,  , the expression
for the sound speed,
, the expression
for the sound speed,
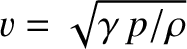 , yields
, yields
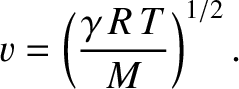 |
(6.14) |
We conclude that the speed of sound in an ideal gas is independent
of the pressure or the density, proportional to the square root of the absolute temperature,
and inversely proportional to the square root of the molecular mass. Incidentally, the root-mean-square molecular
speed in an ideal gas in thermal equilibrium is
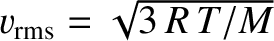 (Reif 2008). Hence, the speed of
sound in an ideal gas is of order, but slightly less than (because the maximum possible value of
(Reif 2008). Hence, the speed of
sound in an ideal gas is of order, but slightly less than (because the maximum possible value of  is
is 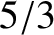 ), the
mean molecular speed.
), the
mean molecular speed.
A comparison between Equations (6.6) and (6.11) reveals that standing
waves and traveling waves in a given medium satisfy the same dispersion relation. However, because traveling waves in infinite media are not subject to boundary constraints, there is no restriction on the possible wavenumbers, or wavelengths,
of such waves. Hence, any traveling wave solution whose wavenumber,  , and
angular frequency,
, and
angular frequency,  , are related according to the dispersion relation
(6.11) is a valid solution of the wave equation. In other words,
any traveling wave solution whose wavelength,
, are related according to the dispersion relation
(6.11) is a valid solution of the wave equation. In other words,
any traveling wave solution whose wavelength,
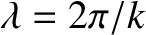 , and frequency,
, and frequency,
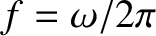 , are related according to
, are related according to
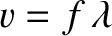 |
(6.15) |
is a valid solution. We conclude that relatively high-frequency traveling waves propagating through a given medium possess relatively
short wavelengths, and vice versa.
Consider the alternative wave solution
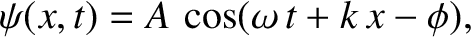 |
(6.16) |
where 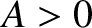 ,
, 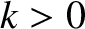 ,
, 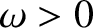 , and
, and  are constants. As before,
this solution is interpreted as a wave of amplitude
are constants. As before,
this solution is interpreted as a wave of amplitude 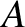 , wavenumber
, wavenumber  , angular frequency
, angular frequency  ,
and phase angle
,
and phase angle  .
However, the wave maxima are now located at
.
However, the wave maxima are now located at
 |
(6.17) |
where  is an integer, and have equations of motion of the form
is an integer, and have equations of motion of the form
 |
(6.18) |
Equation (6.16), thus, represents a traveling wave that propagates in the minus
 -direction at the phase velocity
-direction at the phase velocity
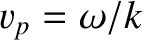 .
Moreover, substitution of Equation (6.16) into the wave equation, (6.1), again
yields the dispersion relation (6.11), which implies that
.
Moreover, substitution of Equation (6.16) into the wave equation, (6.1), again
yields the dispersion relation (6.11), which implies that 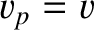 .
It follows that traveling wave solutions to
the wave equation, (6.1), can propagate in either the positive or the negative
.
It follows that traveling wave solutions to
the wave equation, (6.1), can propagate in either the positive or the negative  -direction, as long as they always travel at the fixed speed
-direction, as long as they always travel at the fixed speed  .
.
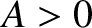 ,
, 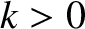 ,
, 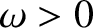 , and
, and  are constants. This solution is interpreted as a wave of amplitude
are constants. This solution is interpreted as a wave of amplitude 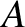 , wavenumber
, wavenumber  , wavelength
, wavelength
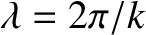 , angular frequency
, angular frequency  , frequency (in hertz)
, frequency (in hertz)
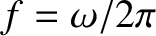 , period
, period 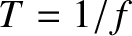 , and phase angle
, and phase angle  . It can be seen that
. It can be seen that
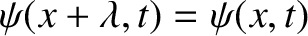 , and
, and
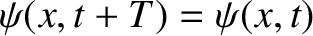 ,
for all
,
for all  and
and  . In other words, the wave is periodic in space with period
. In other words, the wave is periodic in space with period  ,
and periodic in time with period
,
and periodic in time with period  . A wave maximum corresponds to
a point at which
. A wave maximum corresponds to
a point at which
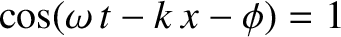 . It follows, from the well-known
properties of the cosine function, that the various wave maxima are located at
. It follows, from the well-known
properties of the cosine function, that the various wave maxima are located at
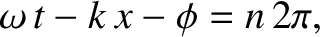
 is an integer. Differentiating the previous expression with respect to
is an integer. Differentiating the previous expression with respect to  ,
and rearranging, the equation of motion of a particular maximum becomes
,
and rearranging, the equation of motion of a particular maximum becomes
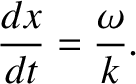
 -axis at the
velocity
-axis at the
velocity
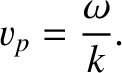
 -axis at the same velocity. In fact, the whole wave pattern
propagates in the positive
-axis at the same velocity. In fact, the whole wave pattern
propagates in the positive  -direction without changing shape. The characteristic propagation velocity
-direction without changing shape. The characteristic propagation velocity 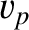 is known as the phase velocity, because
it is the velocity of constant phase points on the wave disturbance (i.e., points that satisfy
is known as the phase velocity, because
it is the velocity of constant phase points on the wave disturbance (i.e., points that satisfy
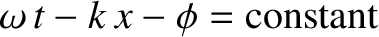 ). For obvious reasons, the type of wave solution specified in Equation (6.7) is called a traveling
wave.
). For obvious reasons, the type of wave solution specified in Equation (6.7) is called a traveling
wave.
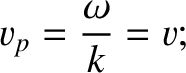
 .
It follows that the constant
.
It follows that the constant 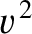 , that appears in the wave
equation, (6.1), can be interpreted as the square of the velocity with which traveling waves propagate through the
medium in question. Hence, from the discussions in Sections 4.3, 5.2, and 5.3, transverse waves propagate along strings of tension
, that appears in the wave
equation, (6.1), can be interpreted as the square of the velocity with which traveling waves propagate through the
medium in question. Hence, from the discussions in Sections 4.3, 5.2, and 5.3, transverse waves propagate along strings of tension  and
mass per unit length
and
mass per unit length  at the phase velocity
at the phase velocity
 , longitudinal
waves propagate along thin elastic rods of Young's modulus
, longitudinal
waves propagate along thin elastic rods of Young's modulus 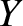 and mass density
and mass density
 at the phase velocity
at the phase velocity
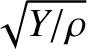 , and sound waves propagate
through ideal gases of pressure
, and sound waves propagate
through ideal gases of pressure 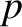 , mass density
, mass density  , and ratio of specific heats
, and ratio of specific heats  , at the phase velocity
, at the phase velocity
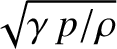 .
.
 and molecular weight
and molecular weight  satisfies the
ideal gas equation of state,
satisfies the
ideal gas equation of state,
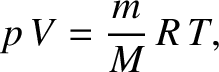
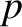 is the pressure,
is the pressure, 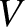 the volume,
the volume,
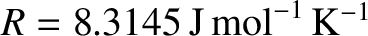 the molar ideal gas constant, and
the molar ideal gas constant, and  the
absolute temperature (Reif 2008). Because the ratio
the
absolute temperature (Reif 2008). Because the ratio 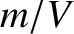 is equal to the density,
is equal to the density,  , the expression
for the sound speed,
, the expression
for the sound speed,
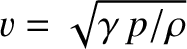 , yields
, yields
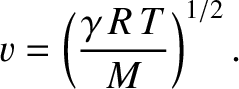
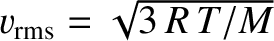 (Reif 2008). Hence, the speed of
sound in an ideal gas is of order, but slightly less than (because the maximum possible value of
(Reif 2008). Hence, the speed of
sound in an ideal gas is of order, but slightly less than (because the maximum possible value of  is
is 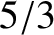 ), the
mean molecular speed.
), the
mean molecular speed.
 , and
angular frequency,
, and
angular frequency,  , are related according to the dispersion relation
(6.11) is a valid solution of the wave equation. In other words,
any traveling wave solution whose wavelength,
, are related according to the dispersion relation
(6.11) is a valid solution of the wave equation. In other words,
any traveling wave solution whose wavelength,
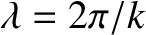 , and frequency,
, and frequency,
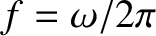 , are related according to
, are related according to
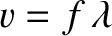
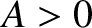 ,
, 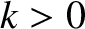 ,
, 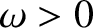 , and
, and  are constants. As before,
this solution is interpreted as a wave of amplitude
are constants. As before,
this solution is interpreted as a wave of amplitude 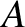 , wavenumber
, wavenumber  , angular frequency
, angular frequency  ,
and phase angle
,
and phase angle  .
However, the wave maxima are now located at
.
However, the wave maxima are now located at

 is an integer, and have equations of motion of the form
is an integer, and have equations of motion of the form

 -direction at the phase velocity
-direction at the phase velocity
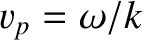 .
Moreover, substitution of Equation (6.16) into the wave equation, (6.1), again
yields the dispersion relation (6.11), which implies that
.
Moreover, substitution of Equation (6.16) into the wave equation, (6.1), again
yields the dispersion relation (6.11), which implies that 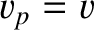 .
It follows that traveling wave solutions to
the wave equation, (6.1), can propagate in either the positive or the negative
.
It follows that traveling wave solutions to
the wave equation, (6.1), can propagate in either the positive or the negative  -direction, as long as they always travel at the fixed speed
-direction, as long as they always travel at the fixed speed  .
.