Next: Exercises Up: Wave Optics Previous: Diffraction from Circular Aperture Contents
![\includegraphics[width=1\textwidth]{Chapter10/fig10_21.eps}](img3713.png) |
Finally, consider the diffraction pattern of a circular disk of radius  whose center lies
at
whose center lies
at 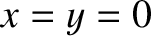 . Because the disk is complementary to
the circular aperture discussed in the previous section, we can use Babinet's principle (see Section 10.11)
to deduce that
. Because the disk is complementary to
the circular aperture discussed in the previous section, we can use Babinet's principle (see Section 10.11)
to deduce that
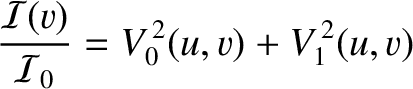 |
(10.163) |
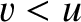 , and
, and
![$\displaystyle \frac{{\cal I}(v)}{{\cal I}_0}= \left[U_1(u,v)-\sin\left(\frac{u^...
...{\,2}+\left[U_2(u,v)-\cos\left(\frac{u^{\,2}+v^{\,2}}{2\,u}\right)\right]^{\,2}$](img3715.png) |
(10.164) |
 .
.
Figure 10.21 shows a typical far-field (i.e., 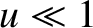 ) and near-field (i.e.,
) and near-field (i.e., 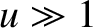 )
diffraction pattern of a circular disk, as determined by the previous two formulae.
)
diffraction pattern of a circular disk, as determined by the previous two formulae.
It
can be seen that the far-field diffraction pattern is an axially symmetric version of the
far-field diffraction pattern of a thin wire, which was discussed in Section 10.15. To
be more exact, the far-field diffraction pattern consists of a central bright disk surrounded by
concentric diffraction fringes. As is clear from Exercise 24, the centers of the fringes correspond (approximately) to the maxima of the function
![$J_1[2\pi\,a\,r'/(\lambda\,R)]$](img3717.png) . Hence, it is
possible to determine the diameter of
a circular disk (or a sphere) from its diffraction pattern.
. Hence, it is
possible to determine the diameter of
a circular disk (or a sphere) from its diffraction pattern.
In the near-field limit, 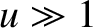 , the
diffraction pattern of the disk is essentially a geometric shadow, bounded by a circular
straight-edge diffraction pattern. (See Section 10.13.) Note, however, that there is a bright
spot at the center of the shadow. In fact, it can be demonstrated (see Exercise 24) that the
central intensity of the diffraction pattern is the same as that of the light illuminating the disk [i.e.,
, the
diffraction pattern of the disk is essentially a geometric shadow, bounded by a circular
straight-edge diffraction pattern. (See Section 10.13.) Note, however, that there is a bright
spot at the center of the shadow. In fact, it can be demonstrated (see Exercise 24) that the
central intensity of the diffraction pattern is the same as that of the light illuminating the disk [i.e.,
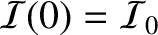 ], irrespective
of the disk's radius (i.e., for all values of
], irrespective
of the disk's radius (i.e., for all values of 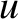 ). This is one of the most famous results in optics.
). This is one of the most famous results in optics.
At the beginning of the 19th century, most scientists favored Isaac Newton's corpuscular theory of light; among these was the theoretician Siméon Denis Poisson (Wikipedia contributors 2018). In 1818, the French Academy of Sciences launched a competition to explain the properties of light, and Poisson was one of the members of the judging committee. The civil engineer Augustin-Jean Fresnel entered this competition by submitting a new wave theory of light. Poisson studied Fresnel's theory in detail, and, being a supporter of the particle theory of light, looked for a way to prove it wrong. Poisson thought that he had found a flaw when he argued that one consequence of Fresnel's theory was that there would exist an on-axis bright spot in the shadow of a circular obstacle, where there should be complete darkness according to the particle theory of light. Because this spot is not easily observed in everyday situations, Poisson interpreted it as an absurd result that disproved Fresnel's theory. However, the head of the committee, Dominique-François-Jean Arago (who incidentally later became Prime Minister of France) decided to perform the experiment in more detail. He succeeded in observing the predicted spot, which convinced most scientists of the wave nature of light, and gave Fresnel victory in the competition. Ever since, the spot in question has been known, somewhat ironically, as Poisson's spot.