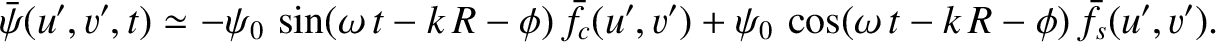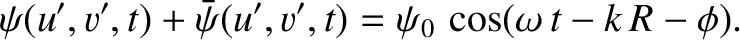Babinet's Principle
Suppose that a given aperture is characterized by the aperture function 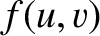 .
Consider a so-called complementary aperture whose aperture function,
.
Consider a so-called complementary aperture whose aperture function,
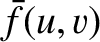 , satisfies
, satisfies
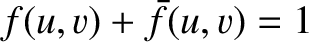 |
(10.111) |
for all 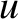 and
and 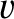 . In other words, the complementary aperture is transparent everywhere where the
original aperture is opaque, and vice versa. Let
It is clear from the analysis in the previous section that
Let
. In other words, the complementary aperture is transparent everywhere where the
original aperture is opaque, and vice versa. Let
It is clear from the analysis in the previous section that
Let
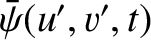 denote the wave amplitude at the projection screen when the complementary
aperture is illuminated. By analogy with Equation (10.102),
denote the wave amplitude at the projection screen when the complementary
aperture is illuminated. By analogy with Equation (10.102),
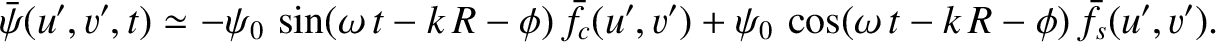 |
(10.116) |
Thus, it follows from Equation (10.102), and the previous three equations, that
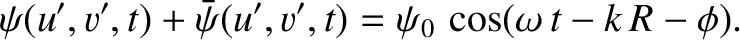 |
(10.117) |
In other words, the sum of the wave amplitude at the projection screen seen when the original aperture
is illuminated and the wave amplitude seen when the complementary aperture is illuminated is equal to the wave
amplitude seen when the aperture is completely transparent. This result is known as
Babinet's principle.
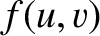 .
Consider a so-called complementary aperture whose aperture function,
.
Consider a so-called complementary aperture whose aperture function,
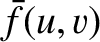 , satisfies
, satisfies
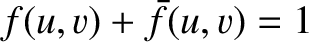
 and
and  . In other words, the complementary aperture is transparent everywhere where the
original aperture is opaque, and vice versa. Let
. In other words, the complementary aperture is transparent everywhere where the
original aperture is opaque, and vice versa. Let
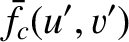
![$\displaystyle =\frac{1}{2}\int_{-\infty}^\infty \bar{f}(u,v)\,\cos\left[\frac{\pi}{2}\,(u-u')^{\,2} +\frac{\pi}{2}\,(v-v')^{\,2}\right]
du\,dv,$](img3603.png)

![$\displaystyle =\frac{1}{2}\int_{-\infty}^\infty \bar{f}(u,v)\,\sin\left[\frac{\pi}{2}\,(u-u')^{\,2} +\frac{\pi}{2}\,(v-v')^{\,2}\right]
du\,dv.$](img3605.png)
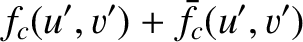
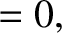


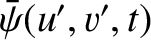 denote the wave amplitude at the projection screen when the complementary
aperture is illuminated. By analogy with Equation (10.102),
denote the wave amplitude at the projection screen when the complementary
aperture is illuminated. By analogy with Equation (10.102),