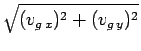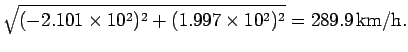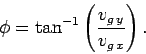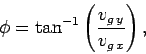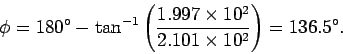Next: Worked example 3.1: Broken
Up: Motion in 3 dimensions
Previous: Projectile motion
Suppose that, on a windy day, an airplane moves with constant velocity 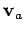 with respect to the
air, and that the air moves with constant velocity
with respect to the
air, and that the air moves with constant velocity 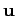 with
respect to the ground. What is the vector velocity
with
respect to the ground. What is the vector velocity 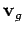 of the plane
with respect to the ground? In principle, the answer to this question is
very simple:
of the plane
with respect to the ground? In principle, the answer to this question is
very simple:
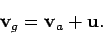 |
(81) |
In other words, the velocity of the plane with respect to the ground is
the vector sum of the plane's velocity relative to the air and the air's
velocity relative to the ground. See Fig. 18. Note that, in general, 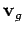 is parallel to neither
is parallel to neither 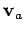 nor
nor 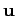 . Let us now consider how we might
implement Eq. (81) in practice.
. Let us now consider how we might
implement Eq. (81) in practice.
Figure 18:
Relative velocity
 |
As always, our first task is to set up a suitable Cartesian coordinate system.
A convenient system for dealing with 2-dimensional motion parallel to the Earth's surface
is illustrated in Fig. 19. The  -axis points northward, whereas the
-axis points northward, whereas the  -axis points
eastward. In this coordinate system, it is conventional to specify a vector
-axis points
eastward. In this coordinate system, it is conventional to specify a vector  in
term of its magnitude,
in
term of its magnitude,  , and its compass bearing,
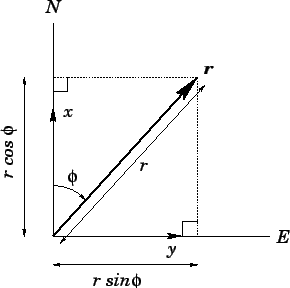
, and its compass bearing, 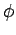 . As illustrated in Fig. 20,
a compass bearing is the angle subtended between the direction of a vector and the direction to
the North pole: i.e., the
. As illustrated in Fig. 20,
a compass bearing is the angle subtended between the direction of a vector and the direction to
the North pole: i.e., the  -direction. By convention, compass bearings
run from
-direction. By convention, compass bearings
run from 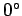 to
to 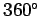 . Furthermore, the compass bearings of North, East, South, and West
are
. Furthermore, the compass bearings of North, East, South, and West
are 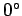 ,
, 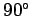 ,
, 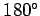 , and
, and  , respectively.
, respectively.
Figure 19:
Coordinates for relative velocity problem
 |
According to Fig. 20, the components of
a general vector  , whose magnitude is
, whose magnitude is  and whose compass bearing is
and whose compass bearing is 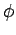 , are simply
, are simply
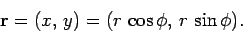 |
(82) |
Note that we have suppressed the  -component of
-component of  (which is zero), for ease of
notation. Although, strictly speaking, Fig. 20 only justifies the above expression for
(which is zero), for ease of
notation. Although, strictly speaking, Fig. 20 only justifies the above expression for
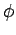 in the range
in the range 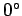 to
to 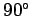 , it turns out that this expression
is generally valid: i.e., it is valid for
, it turns out that this expression
is generally valid: i.e., it is valid for 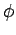 in the full range
in the full range 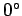 to
to
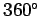 .
.
Figure 20:
A compass bearing
 |
As an illustration, suppose that the plane's velocity relative to the air
is
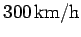 , at a compass bearing of
, at a compass bearing of 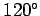 , and
the air's velocity relative to the ground is
, and
the air's velocity relative to the ground is
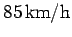 , at a compass
bearing of
, at a compass
bearing of 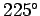 . It follows that the components of
. It follows that the components of 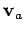 and
and
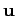 (measured in units of km/h) are
(measured in units of km/h) are
According to Eq. (81), the components of the plane's velocity 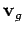 relative to
the ground are simply the algebraic sums of the corresponding components
of
relative to
the ground are simply the algebraic sums of the corresponding components
of 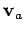 and
and 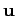 . Hence,
. Hence,
Our final task is to reconstruct the magnitude and compass bearing of vector 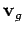 ,
given its components
,
given its components
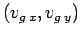 . The magnitude of
. The magnitude of 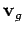 follows
from Pythagoras' theorem [see Eq. (35)]:
follows
from Pythagoras' theorem [see Eq. (35)]:
In principle, the compass bearing of 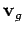 is given
by the following formula:
is given
by the following formula:
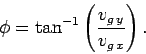 |
(87) |
This follows because
 and
and
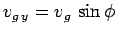 [see
Eq. (82)].
Unfortunately, the above expression becomes a little difficult to interpret
if
[see
Eq. (82)].
Unfortunately, the above expression becomes a little difficult to interpret
if 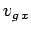 is negative. An unambiguous
pair of expressions for
is negative. An unambiguous
pair of expressions for 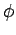 is given below:
is given below:
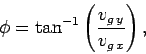 |
(88) |
if
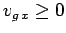 ; or
; or
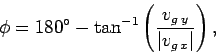 |
(89) |
if  .
These expressions can be derived from simple
trigonometry.
For the case in hand, Eq. (89) is the
relevant expression, hence
.
These expressions can be derived from simple
trigonometry.
For the case in hand, Eq. (89) is the
relevant expression, hence
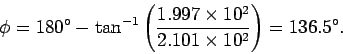 |
(90) |
Thus, the plane's velocity relative to the ground is
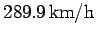 at a compass
bearing of
at a compass
bearing of 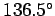 .
.



Next: Worked example 3.1: Broken
Up: Motion in 3 dimensions
Previous: Projectile motion
Richard Fitzpatrick
2006-02-02
![]() -axis points northward, whereas the
-axis points northward, whereas the ![]() -axis points
eastward. In this coordinate system, it is conventional to specify a vector
-axis points
eastward. In this coordinate system, it is conventional to specify a vector ![]() in
term of its magnitude,
in
term of its magnitude, ![]() , and its compass bearing,
, and its compass bearing, ![]() . As illustrated in Fig. 20,
a compass bearing is the angle subtended between the direction of a vector and the direction to
the North pole: i.e., the
. As illustrated in Fig. 20,
a compass bearing is the angle subtended between the direction of a vector and the direction to
the North pole: i.e., the ![]() -direction. By convention, compass bearings
run from
-direction. By convention, compass bearings
run from ![]() to
to ![]() . Furthermore, the compass bearings of North, East, South, and West
are
. Furthermore, the compass bearings of North, East, South, and West
are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
![]() , whose magnitude is
, whose magnitude is ![]() and whose compass bearing is
and whose compass bearing is ![]() , are simply
, are simply
![]() , at a compass bearing of
, at a compass bearing of ![]() , and
the air's velocity relative to the ground is
, and
the air's velocity relative to the ground is
![]() , at a compass
bearing of
, at a compass
bearing of ![]() . It follows that the components of
. It follows that the components of ![]() and
and
![]() (measured in units of km/h) are
(measured in units of km/h) are
![]() ,
given its components
,
given its components
![]() . The magnitude of
. The magnitude of ![]() follows
from Pythagoras' theorem [see Eq. (35)]:
follows
from Pythagoras' theorem [see Eq. (35)]: