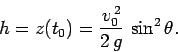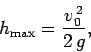Next: Relative velocity
Up: Motion in 3 dimensions
Previous: Motion with constant acceleration
As a simple illustration of the concepts introduced in the previous subsections,
let us examine
the following problem. Suppose that a projectile is launched upward
from ground level, with speed 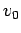 , making an angle
, making an angle  with the horizontal. Neglecting the effect of air resistance, what
is the subsequent trajectory of the projectile?
with the horizontal. Neglecting the effect of air resistance, what
is the subsequent trajectory of the projectile?
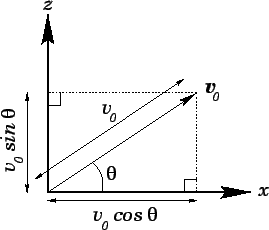
Our first task is to set up a suitable Cartesian coordinate system.
A convenient system is illustrated in Fig. 16. The  -axis points vertically
upwards (this is a standard convention), whereas the
-axis points vertically
upwards (this is a standard convention), whereas the  -axis points along the
projectile's
initial direction of horizontal motion. Furthermore, the origin of our
coordinate system corresponds to the launch point. Thus,
-axis points along the
projectile's
initial direction of horizontal motion. Furthermore, the origin of our
coordinate system corresponds to the launch point. Thus, 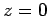 corresponds
to ground level.
corresponds
to ground level.
Neglecting air resistance,
the projectile is subject to a constant acceleration
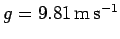 ,
due to gravity, which is directed vertically downwards. Thus, the projectile's
vector acceleration is written
,
due to gravity, which is directed vertically downwards. Thus, the projectile's
vector acceleration is written
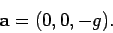 |
(70) |
Here, the minus sign indicates that the acceleration is in the minus  -direction
(i.e., downwards), as opposed to the plus
-direction
(i.e., downwards), as opposed to the plus  -direction (i.e., upwards).
-direction (i.e., upwards).
Figure 16:
Coordinates for the projectile problem
 |
What is the initial vector velocity  with which the projectile is launched
into the air at (say)
with which the projectile is launched
into the air at (say)  ? As illustrated in Fig. 16,
given that the magnitude of this velocity is
? As illustrated in Fig. 16,
given that the magnitude of this velocity is 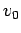 , its horizontal component
is directed along the
, its horizontal component
is directed along the  -axis, and its direction subtends an angle
-axis, and its direction subtends an angle  with this axis, the components of
with this axis, the components of  take the form
take the form
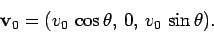 |
(71) |
Note that  has zero component along the
has zero component along the  -axis, which points
into the paper in Fig. 16.
-axis, which points
into the paper in Fig. 16.
Since the projectile moves with constant acceleration, its vector
displacement
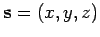 from its launch point
satisfies [see Eq. (64)]
from its launch point
satisfies [see Eq. (64)]
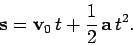 |
(72) |
Making use of Eqs. (70) and (71), the  -,
-,  -, and
-, and  -components
of the above equation are written
-components
of the above equation are written
respectively.
Note that the projectile moves with constant velocity,
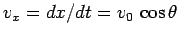 ,
in the
,
in the  -direction (i.e., horizontally). This is hardly surprising, since there
is zero component of the projectile's acceleration along the
-direction (i.e., horizontally). This is hardly surprising, since there
is zero component of the projectile's acceleration along the  -axis. Note, further,
that
since there is zero component of the projectile's acceleration along the
-axis. Note, further,
that
since there is zero component of the projectile's acceleration along the  -axis, and
the projectile's initial velocity also has zero component along this axis,
the projectile never moves in the
-axis, and
the projectile's initial velocity also has zero component along this axis,
the projectile never moves in the  -direction. In other words, the projectile's
trajectory is 2-dimensional, lying entirely within the
-direction. In other words, the projectile's
trajectory is 2-dimensional, lying entirely within the  -
- plane. Note,
finally, that the projectile's vertical motion is entirely decoupled
from its horizontal motion. In other words, the projectile's vertical motion is
identical to that of a second projectile launched vertically upwards, at
plane. Note,
finally, that the projectile's vertical motion is entirely decoupled
from its horizontal motion. In other words, the projectile's vertical motion is
identical to that of a second projectile launched vertically upwards, at  ,
with the initial velocity
,
with the initial velocity
 (i.e., the
initial vertical velocity component of the first projectile)--both projectiles will reach the
same maximum altitude at the same time, and will subsequently strike the ground simultaneously.
(i.e., the
initial vertical velocity component of the first projectile)--both projectiles will reach the
same maximum altitude at the same time, and will subsequently strike the ground simultaneously.
Equations (73) and (75) can be rearranged to give
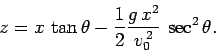 |
(76) |
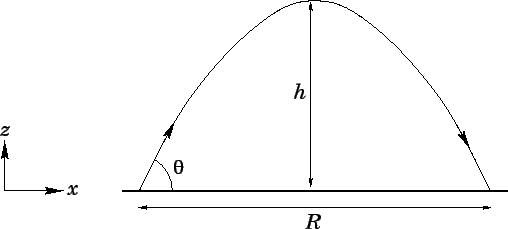
As was first pointed out by Galileo, and is illustrated in Fig. 17, this is
the equation of a parabola. The horizontal range
 of the projectile corresponds to its
of the projectile corresponds to its  -coordinate when it strikes the
ground (i.e., when
-coordinate when it strikes the
ground (i.e., when 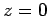 ). It follows from the above
expression (neglecting the trivial result
). It follows from the above
expression (neglecting the trivial result  ) that
) that
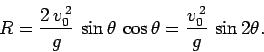 |
(77) |
Note that the range attains its maximum value,
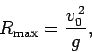 |
(78) |
when
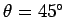 . In other words, neglecting air resistance, a projectile
travels furthest when it is launched into the air at
. In other words, neglecting air resistance, a projectile
travels furthest when it is launched into the air at 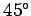 to the horizontal.
to the horizontal.
The maximum altitude 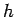 of the projectile is attained when
of the projectile is attained when
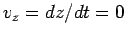 (i.e., when the projectile has just stopped rising and
is about to start falling). It follows from Eq. (75) that the maximum altitude
occurs at time
(i.e., when the projectile has just stopped rising and
is about to start falling). It follows from Eq. (75) that the maximum altitude
occurs at time
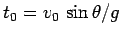 . Hence,
. Hence,
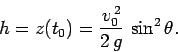 |
(79) |
Obviously, the largest value of 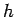 ,
,
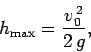 |
(80) |
is obtained when the projectile is launched vertically upwards
(i.e.,
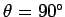 ).
).
Figure 17:
The parabolic trajectory of a projectile
 |



Next: Relative velocity
Up: Motion in 3 dimensions
Previous: Motion with constant acceleration
Richard Fitzpatrick
2006-02-02
![]() -axis points vertically
upwards (this is a standard convention), whereas the
-axis points vertically
upwards (this is a standard convention), whereas the ![]() -axis points along the
projectile's
initial direction of horizontal motion. Furthermore, the origin of our
coordinate system corresponds to the launch point. Thus,
-axis points along the
projectile's
initial direction of horizontal motion. Furthermore, the origin of our
coordinate system corresponds to the launch point. Thus, ![]() corresponds
to ground level.
corresponds
to ground level.
![]() ,
due to gravity, which is directed vertically downwards. Thus, the projectile's
vector acceleration is written
,
due to gravity, which is directed vertically downwards. Thus, the projectile's
vector acceleration is written
![]() with which the projectile is launched
into the air at (say)
with which the projectile is launched
into the air at (say) ![]() ? As illustrated in Fig. 16,
given that the magnitude of this velocity is
? As illustrated in Fig. 16,
given that the magnitude of this velocity is ![]() , its horizontal component
is directed along the
, its horizontal component
is directed along the ![]() -axis, and its direction subtends an angle
-axis, and its direction subtends an angle ![]() with this axis, the components of
with this axis, the components of ![]() take the form
take the form
![]() from its launch point
satisfies [see Eq. (64)]
from its launch point
satisfies [see Eq. (64)]
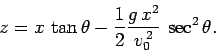
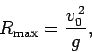
![]() of the projectile is attained when
of the projectile is attained when
![]() (i.e., when the projectile has just stopped rising and
is about to start falling). It follows from Eq. (75) that the maximum altitude
occurs at time
(i.e., when the projectile has just stopped rising and
is about to start falling). It follows from Eq. (75) that the maximum altitude
occurs at time
![]() . Hence,
. Hence,