


Next: Projectile motion
Up: Motion in 3 dimensions
Previous: Motion with constant velocity
Motion with constant acceleration
An object moving in 3 dimensions with constant acceleration  possesses a vector displacement of the form
possesses a vector displacement of the form
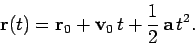 |
(62) |
Hence, the object's velocity is given by
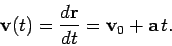 |
(63) |
Note that
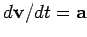 , as expected. In the above,
the constant vectors
, as expected. In the above,
the constant vectors 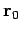 and
and  are the object's displacement and velocity at time
are the object's displacement and velocity at time
 , respectively.
, respectively.
As is easily demonstrated, the vector equivalents of Eqs. (21)-(23) are:
These equation fully characterize 3-dimensional motion with constant acceleration.
Here,
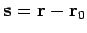 is the net displacement of the object
between times
is the net displacement of the object
between times  and
and  .
.
The quantity
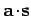 , appearing in Eq. (66), is termed
the scalar product of vectors
, appearing in Eq. (66), is termed
the scalar product of vectors  and
and 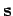 , and is defined
, and is defined
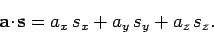 |
(67) |
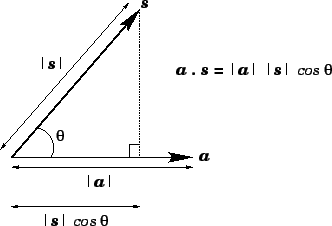
The above formula has a simple geometric interpretation, which is illustrated
in Fig. 15. If  is the magnitude (or length) of vector
is the magnitude (or length) of vector  ,
,
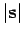 is the magnitude of vector
is the magnitude of vector 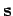 , and
, and  is the angle
subtended between these two vectors, then
is the angle
subtended between these two vectors, then
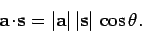 |
(68) |
In other words, the scalar product of vectors  and
and 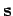 equals
the product of the length of vector
equals
the product of the length of vector  times the length of that component of
vector
times the length of that component of
vector 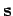 which lies in the same direction as vector
which lies in the same direction as vector  .
It immediately follows that if two vectors are mutually perpendicular
(i.e.,
.
It immediately follows that if two vectors are mutually perpendicular
(i.e.,
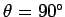 ) then their scalar product is zero. Furthermore, the
scalar product of a vector with itself is simply the magnitude squared of that vector [this
is immediately apparent from Eq. (67)]:
) then their scalar product is zero. Furthermore, the
scalar product of a vector with itself is simply the magnitude squared of that vector [this
is immediately apparent from Eq. (67)]:
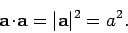 |
(69) |
It is also apparent from Eq. (67) that
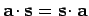 ,
and
,
and
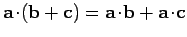 ,
and
,
and
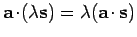 .
.
Figure 15:
The scalar product
 |
Incidentally, Eq. (66) is obtained by taking the scalar product of Eq. (65) with itself,
taking the scalar product of Eq. (64) with  , and then eliminating
, and then eliminating  .
.



Next: Projectile motion
Up: Motion in 3 dimensions
Previous: Motion with constant velocity
Richard Fitzpatrick
2006-02-02
![]() , appearing in Eq. (66), is termed
the scalar product of vectors
, appearing in Eq. (66), is termed
the scalar product of vectors ![]() and
and ![]() , and is defined
, and is defined
![]() , and then eliminating
, and then eliminating ![]() .
.