Next: Worked example 3.2: Gallileo's
Up: Motion in 3 dimensions
Previous: Relative velocity
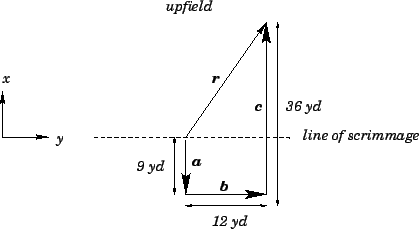
Question: Major Applewhite receives the snap at the line
of scrimmage, takes a seven step drop (i.e., runs backwards
9 yards), but is then flushed out of the pocket by a blitzing
linebacker. Major subsequently runs parallel to the line of scrimmage
for 12 yards and then gets off a forward pass, 36 yards straight downfield, to
Roy Williams, just prior to being creamed by the linebacker. What is the magnitude
of the football's resultant displacement (in yards)?
Answer: As illustrated in the diagram, the resultant displacement  of the
football is the sum of vectors
of the
football is the sum of vectors  ,
, 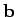 , and
, and 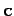 , which
correspond to the seven step drop, the run parallel to the line of
scrimmage, and the forward pass, respectively.
Using the coordinate system indicated in the diagram, the components of
vectors
, which
correspond to the seven step drop, the run parallel to the line of
scrimmage, and the forward pass, respectively.
Using the coordinate system indicated in the diagram, the components of
vectors  ,
, 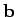 , and
, and 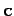 (measured in yards) are
(measured in yards) are
respectively. Hence the components of  are given by
are given by
It follows that the magnitude of the football's resultant displacement is



Next: Worked example 3.2: Gallileo's
Up: Motion in 3 dimensions
Previous: Relative velocity
Richard Fitzpatrick
2006-02-02