Vector magnitude

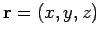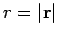If ${\bf r}=(x,y,z)$ represents the vector displacement of point $R$ from the origin, what is the distance between these two points? In other words, what is the length, or magnitude, $r=\vert{\bf r}\vert$, of vector ${\bf r}$. It follows from a 3-dimensional generalization of Pythagoras' theorem that

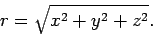$$r = \sqrt{x^2+ y^2 + z^2}.$$ (35)

Note that if 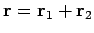${\bf r}= {\bf r}_1 + {\bf r}_2$ then

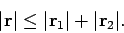$$\vert{\bf r}\vert \leq \vert{\bf r}_1\vert + \vert{\bf r}_2\vert.$$ (36)

In other words, the magnitudes of vectors cannot, in general, be added algebraically. The only exception to this rule (represented by the equality sign in the above expression) occurs when the vectors in question all point in the same direction. According to inequality (36), if we move 1m to the North (say) and next move 1m to the West (say) then, although we have moved a total distance of 2m, our net distance from the starting point is less than 2m--of course, this is just common sense.