


Next: Vector magnitude
Up: Motion in 3 dimensions
Previous: Vector displacement
Suppose that the vector displacement
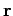 of some point
of some point 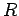 from the origin
from the origin 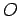 is specified as follows:
is specified as follows:
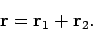 |
(31) |
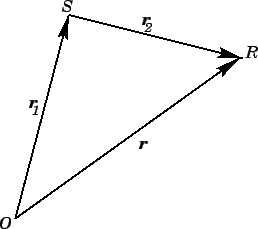
Figure 12 illustrates how this expression is interpreted diagrammatically: in order to
get from point 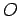 to point
to point 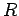 , we first move from point
, we first move from point 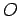 to point
to point 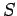 along vector
along vector
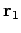 , and we then move from point
, and we then move from point 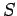 to point
to point 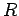 along vector
along vector 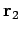 . The
net result is the same as if we had moved from point
. The
net result is the same as if we had moved from point 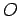 directly to point
directly to point 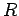 along
vector
along
vector 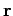 . Vector
. Vector 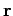 is termed the resultant of adding vectors
is termed the resultant of adding vectors
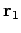 and
and 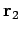 .
.
Figure 12:
Vector addition
 |
Note that we have two ways of specifying the vector displacement of point  from
the origin: we can either write
from
the origin: we can either write 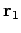 or
or
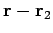 . The
expression
. The
expression
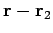 is interpreted as follows: starting at the origin,
move along vector
is interpreted as follows: starting at the origin,
move along vector 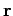 in the direction of the arrow, then move along
vector
in the direction of the arrow, then move along
vector 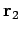 in the opposite direction to the arrow. In other words,
a minus sign in front of a vector indicates that we should move along that vector in
the opposite direction to its arrow.
in the opposite direction to the arrow. In other words,
a minus sign in front of a vector indicates that we should move along that vector in
the opposite direction to its arrow.
Suppose that the components of vectors 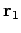 and
and 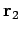 are
are
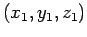 and
and
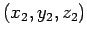 , respectively. As is easily demonstrated,
the components
, respectively. As is easily demonstrated,
the components 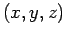 of the
resultant vector
of the
resultant vector
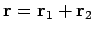 are
are
In other words, the components of the sum of two vectors are simply the algebraic
sums of the components of the individual vectors.



Next: Vector magnitude
Up: Motion in 3 dimensions
Previous: Vector displacement
Richard Fitzpatrick
2006-02-02
![]() from
the origin: we can either write
from
the origin: we can either write ![]() or
or
![]() . The
expression
. The
expression
![]() is interpreted as follows: starting at the origin,
move along vector
is interpreted as follows: starting at the origin,
move along vector ![]() in the direction of the arrow, then move along
vector
in the direction of the arrow, then move along
vector ![]() in the opposite direction to the arrow. In other words,
a minus sign in front of a vector indicates that we should move along that vector in
the opposite direction to its arrow.
in the opposite direction to the arrow. In other words,
a minus sign in front of a vector indicates that we should move along that vector in
the opposite direction to its arrow.
![]() and
and ![]() are
are
![]() and
and
![]() , respectively. As is easily demonstrated,
the components
, respectively. As is easily demonstrated,
the components ![]() of the
resultant vector
of the
resultant vector
![]() are
are