


Next: Vector addition
Up: Motion in 3 dimensions
Previous: Cartesian coordinates
Consider the motion of a body moving in 3 dimensions. The
body's instantaneous
position is most conveniently specified by giving its displacement from the origin of our
coordinate system. Note, however, that in 3 dimensions such a displacement possesses both
magnitude and direction. In other words, we not only have to
specify how far the body is situated from the origin, we also
have to specify in which direction it lies. A quantity which possesses both
magnitude and direction is termed a vector. By contrast, a quantity
which possesses only magnitude is termed a scalar. Mass and time are scalar
quantities. However, in general, displacement is a vector.
The vector displacement 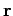 of some point
of some point 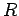 from the origin
from the origin 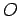 can be visualized as an arrow running from point
can be visualized as an arrow running from point 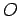 to point
to point 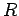 . See Fig. 11.
Note that in typeset documents vector quantities are conventionally written in a bold-faced font
(e.g.,
. See Fig. 11.
Note that in typeset documents vector quantities are conventionally written in a bold-faced font
(e.g., 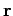 ) to
distinguish them from scalar quantities. In free-hand notation, vectors are usually
under-lined (e.g.,
) to
distinguish them from scalar quantities. In free-hand notation, vectors are usually
under-lined (e.g., 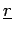 ).
).
Figure 11:
A vector displacement
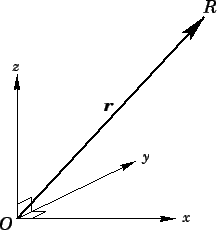 |
The vector displacement 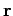 can also be specified in terms of its coordinates:
can also be specified in terms of its coordinates:
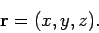 |
(30) |
The above expression is interpreted as follows: in order to get from point  to
point
to
point  , first move
, first move  meters along the
meters along the  -axis (perpendicular to both the
-axis (perpendicular to both the 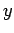 - and
- and 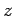 -axes),
then move
-axes),
then move 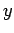 meters along the
meters along the 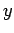 -axis (perpendicular to both the
-axis (perpendicular to both the  - and
- and 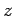 -axes),
finally move
-axes),
finally move 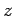 meters along the
meters along the 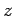 -axis (perpendicular to both the
-axis (perpendicular to both the  - and
- and 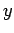 -axes).
Note that a positive
-axes).
Note that a positive  value is interpreted as an instruction to move
value is interpreted as an instruction to move  meters
along the
meters
along the  -axis in the direction of increasing
-axis in the direction of increasing  , whereas
a negative
, whereas
a negative  value is interpreted as an
instruction to move
value is interpreted as an
instruction to move 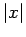 meters
along the
meters
along the  -axis in the opposite direction, and so on.
-axis in the opposite direction, and so on.



Next: Vector addition
Up: Motion in 3 dimensions
Previous: Cartesian coordinates
Richard Fitzpatrick
2006-02-02
![]() of some point
of some point ![]() from the origin
from the origin ![]() can be visualized as an arrow running from point
can be visualized as an arrow running from point ![]() to point
to point ![]() . See Fig. 11.
Note that in typeset documents vector quantities are conventionally written in a bold-faced font
(e.g.,
. See Fig. 11.
Note that in typeset documents vector quantities are conventionally written in a bold-faced font
(e.g., ![]() ) to
distinguish them from scalar quantities. In free-hand notation, vectors are usually
under-lined (e.g.,
) to
distinguish them from scalar quantities. In free-hand notation, vectors are usually
under-lined (e.g., ![]() ).
).
![]() can also be specified in terms of its coordinates:
can also be specified in terms of its coordinates: