next up previous
Next: Diagonals of a parallelogram Up: Motion in 3 dimensions Previous: Vector magnitude

Scalar multiplication

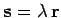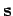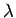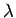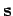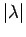Suppose that ${\bf s} = \lambda {\bf r}$. This expression is interpreted as follows: vector ${\bf s}$ points in the same direction as vector ${\bf r}$, but the length of the former vector is $\lambda$ times that of the latter. Note that if $\lambda$ is negative then vector ${\bf s}$ points in the opposite direction to vector ${\bf r}$, and the length of the former vector is $\vert\lambda\vert$ times that of the latter. In terms of components:
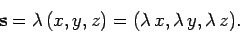\begin{displaymath} {\bf s} = \lambda (x,y,z) = (\lambda x, \lambda y, \lambda z). \end{displaymath} (37)

In other words, when we multiply a vector by a scalar then the components of the resultant vector are obtained by multiplying all the components of the original vector by the scalar.


Richard Fitzpatrick 2006-02-02