


Next: Lunar Parallax
Up: The Moon
Previous: Example Longitude Calculations
A model of the moon's ecliptic latitude is needed in order to predict the
occurrence of solar and lunar eclipses. Figure 23 shows the
moon's orbit about the earth. The plane of this orbit is fixed, but slightly tilted with
respect to the plane of the ecliptic (i.e., the plane of the sun's
apparent orbit about the earth). Let the two planes intersect along the
line of nodes,  . Here,
. Here, 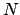 is the point at which the orbit crosses the
ecliptic plane from south to north (in the direction of the moon's orbital
motion), and is termed the ascending node. Likewise,
is the point at which the orbit crosses the
ecliptic plane from south to north (in the direction of the moon's orbital
motion), and is termed the ascending node. Likewise, 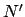 is the
point at which the orbit crosses the ecliptic plane from north to south,
and is called the descending node. Incidentally, the line of nodes must pass through point
is the
point at which the orbit crosses the ecliptic plane from north to south,
and is called the descending node. Incidentally, the line of nodes must pass through point 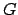 , since the earth is common to the ecliptic plane and the plane of the lunar orbit.
The angle,
, since the earth is common to the ecliptic plane and the plane of the lunar orbit.
The angle,  , subtended between
the radius vector
, subtended between
the radius vector 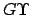 , connecting the earth to the vernal equinox,
and the line
, connecting the earth to the vernal equinox,
and the line  , is known as the longitude of the ascending node. Note, incidentally, that
the ascending node precessess in the opposite direction to the moon's orbital motion
at the rate
, is known as the longitude of the ascending node. Note, incidentally, that
the ascending node precessess in the opposite direction to the moon's orbital motion
at the rate
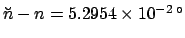 per day, or
per day, or  in 18.6 years.
This unusually large precession rate is another consequence of the sun's strong perturbing influence on the
moon's orbit.
Let the line
in 18.6 years.
This unusually large precession rate is another consequence of the sun's strong perturbing influence on the
moon's orbit.
Let the line 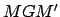 lie in the plane
of the moon's orbit such that it is perpendicular to
lie in the plane
of the moon's orbit such that it is perpendicular to  .
The inclination,
.
The inclination, 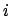 , of the moon's orbital plane is the angle
that
, of the moon's orbital plane is the angle
that 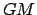 subtends with its projection onto the ecliptic plane. Likewise, the
moon's ecliptic longitude,
subtends with its projection onto the ecliptic plane. Likewise, the
moon's ecliptic longitude, 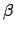 , is the angle that
, is the angle that  subtends with its
projection onto the ecliptic plane.
Simple geometry
yields
subtends with its
projection onto the ecliptic plane.
Simple geometry
yields
 , where
, where 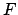 is the angle
between
is the angle
between  and
and  . This angle is termed the argument of latitude.
Now, it is easily seen that
. This angle is termed the argument of latitude.
Now, it is easily seen that
 , where
, where 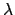 is the moon's ecliptic longitude (i.e., the angle subtended
between
is the moon's ecliptic longitude (i.e., the angle subtended
between 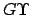 and
and  ). Here, we are assuming that the orbital
inclination
). Here, we are assuming that the orbital
inclination 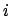 is relatively
small. The mean argument of latitude is defined
is relatively
small. The mean argument of latitude is defined
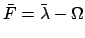 .
Hence, our model for the moon's ecliptic latitude becomes
.
Hence, our model for the moon's ecliptic latitude becomes
The value of the lunar orbital inclination, 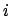 , for the
J2000 epoch is specified in Table 35. The above model is capable of
matching NASA ephemeris data during the years 1995-2006 CE with
a mean error of
, for the
J2000 epoch is specified in Table 35. The above model is capable of
matching NASA ephemeris data during the years 1995-2006 CE with
a mean error of 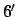 , and a maximum error of
, and a maximum error of 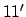 .
.
The ecliptic latitude of the moon can be calculated with the aid of Table 38. The procedure for using this table is as follows:
- Determine the fractional Julian day number,
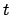 , corresponding to the date and time
at which the moon's ecliptic latitude is to be calculated with the aid of Tables 27-29. Form
, corresponding to the date and time
at which the moon's ecliptic latitude is to be calculated with the aid of Tables 27-29. Form
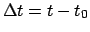 , where
, where
 is the epoch.
is the epoch.
- Calculate the lunar mean argument of latitude,
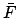 ,
and the five lunar anomalies,
,
and the five lunar anomalies, 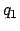 -
-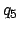 , using the procedure outlined earlier in this
section.
, using the procedure outlined earlier in this
section.
- Form the argument
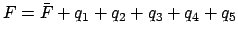 . Add as many multiples of
. Add as many multiples of  to
to 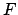 as is required to make it fall in the range
as is required to make it fall in the range
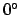 to
to  . Round
. Round 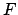 to the nearest degree.
to the nearest degree.
- Enter Table 38 with the value of
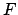 and take out the lunar ecliptic latitude,
and take out the lunar ecliptic latitude, 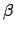 . It is necessary to
interpolate if
. It is necessary to
interpolate if 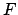 is odd.
is odd.
For example, we have already seen that at 00:00 UT on May 5, 2005 CE
the lunar mean argument of latitude, and
the lunar anomalies, were
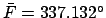 , and
, and
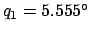 ,
,
 ,
,
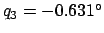 ,
,
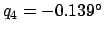 ,
and
,
and
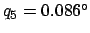 , respectively. Hence,
, respectively. Hence,
 . Thus, according to Table 38, the ecliptic latitude
of the moon at 00:00 UT on May 5, 2005 CE was
. Thus, according to Table 38, the ecliptic latitude
of the moon at 00:00 UT on May 5, 2005 CE was
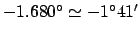 .
.
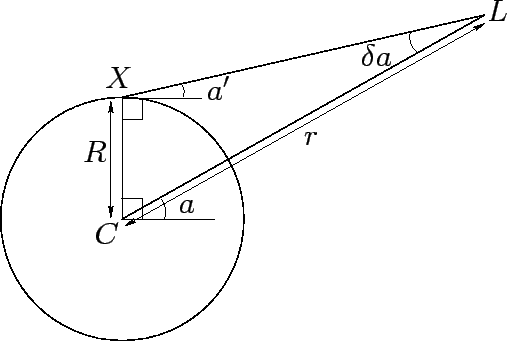
Figure 24:
The moon,  , as viewed by a hypothetical observer,
, as viewed by a hypothetical observer, 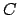 ,
at the center of the earth, and a real observer,
,
at the center of the earth, and a real observer, 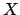 , on the
surface of the earth.
, on the
surface of the earth.
 |



Next: Lunar Parallax
Up: The Moon
Previous: Example Longitude Calculations
Richard Fitzpatrick
2010-07-21
![]() , and
, and
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() , respectively. Hence,
, respectively. Hence,
![]() . Thus, according to Table 38, the ecliptic latitude
of the moon at 00:00 UT on May 5, 2005 CE was
. Thus, according to Table 38, the ecliptic latitude
of the moon at 00:00 UT on May 5, 2005 CE was
![]() .
.
