

Next: Geometric Planetary Orbit Models
Up: Dates
Previous: Introduction
The Julian day number of a given day can be determined from Tables 27-29. The
date must be expressed in terms of the Gregorian calendar.
The procedure is as
follows:
- Enter the table of century years (Table 27) with the century
year immediately preceding the date in question, and take out the tabular
value. If the
century year is marked with a
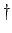 , note this fact for use in step 2.
, note this fact for use in step 2.
- Enter the table of years of the century (Table 28) with the
last two digits of the year in question, and take out the tabular value.
If the century year used in step 1 was marked with a
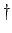 , diminish the tabular value
by one day, unless the tabular value is zero. If the year in question
is a leap year, marked with a
, diminish the tabular value
by one day, unless the tabular value is zero. If the year in question
is a leap year, marked with a 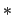 , note this fact for use in step 3.
, note this fact for use in step 3.
- Enter the table of the days of the year (Table 29) with the
day in question, and take out the tabular value. If the year in question
is a leap year and the table entry falls after February 28, add
one day to the tabular value. The sum of the values obtained
in steps 1, 2, and 3 then gives the Julian day number of the date in question.
Example 1: June 10, 1992 CE:
| 1. Century year |
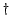 1900 1900 |
|
2415020 |
| 2. Year of the century |
 92 92 |
33603 - 1 = |
33602 |
| 3. Day of the year |
June 10 |
161+1 = |
162 |
| Julian day number |
|
|
2448784 |
| |
|
|
|
Observe that in step 2 the tabular value has been diminished by 1 because 1900
is a common year (marked with a 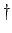 in Table 27). In step 3, the
tabular value has been increased by 1 because 1992 is a leap year (marked with a
in Table 27). In step 3, the
tabular value has been increased by 1 because 1992 is a leap year (marked with a 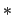 in Table 28), and the
date falls after February 28.
in Table 28), and the
date falls after February 28.
Example 2: January 18, 1824 CE:
| 1. Century year |
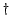 1800 1800 |
|
2378496 |
| 2. Year of the century |
 24 24 |
8766 - 1 = |
8765 |
| 3. Day of the year |
January 18 |
18 = |
18 |
| Julian day number |
|
|
2387279 |
| |
|
|
|
Observe that in step 2 the tabular value has been diminished by 1 because 1800
is a common year (marked with a 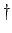 in Table 27). In step 3, the
tabular value has not been increased by 1, despite the fact that 1824 is a leap year (marked with an
in Table 27). In step 3, the
tabular value has not been increased by 1, despite the fact that 1824 is a leap year (marked with an 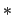 in Table 28), because the
date falls before February 28.
in Table 28), because the
date falls before February 28.
We can specify the time of day (in universal time), as well as the date,
by means of fractional Julian day numbers. For instance,
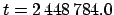 JD corresponds to 12:00 UT on June 10, 1992 CE, whereas
JD corresponds to 12:00 UT on June 10, 1992 CE, whereas
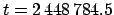 JD corresponds to 24:00 UT later the same day.
JD corresponds to 24:00 UT later the same day.
Table 27:
Julian Day Number: Century Years. 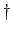 Common years. All years are CE. From ``The History
and Practice of Ancient Astronomy", J. Evans (Oxford University Press, Oxford UK, 1998).
Common years. All years are CE. From ``The History
and Practice of Ancient Astronomy", J. Evans (Oxford University Press, Oxford UK, 1998).
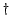 1800 1800 |
2378496 |
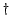 1900 1900 |
2415020 |
| 2000 |
2451544 |
|
Table 28:
Julian Day Number: Years of the Century. 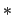 Leap year.
Leap year. 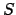 Leap year unless century is marked
Leap year unless century is marked 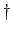 . In centuries marked
. In centuries marked 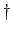 , subtract one day from the tabulated values for the years 1 through 99.
From ``The History
and Practice of Ancient Astronomy", J. Evans (Oxford University Press, Oxford UK, 1998).
, subtract one day from the tabulated values for the years 1 through 99.
From ``The History
and Practice of Ancient Astronomy", J. Evans (Oxford University Press, Oxford UK, 1998).
 0 0 |
0 |
 20 20 |
7305 |
 40 40 |
14610 |
 60 60 |
21915 |
 80 80 |
29220 |
| 1 |
336 |
21 |
7671 |
41 |
14976 |
61 |
22281 |
81 |
29586 |
| 2 |
731 |
22 |
8036 |
42 |
15341 |
62 |
22646 |
82 |
29951 |
| 3 |
1096 |
23 |
8401 |
43 |
15706 |
63 |
22011 |
83 |
30316 |
| |
|
|
|
|
|
|
|
|
|
 4 4 |
1461 |
 24 24 |
8766 |
 44 44 |
16071 |
 64 64 |
23376 |
 84 84 |
30681 |
| 5 |
1827 |
25 |
9132 |
45 |
16437 |
65 |
23742 |
85 |
31047 |
| 6 |
2192 |
26 |
9497 |
46 |
16802 |
66 |
24107 |
86 |
31412 |
| 7 |
2557 |
27 |
9862 |
47 |
17167 |
67 |
24472 |
87 |
31777 |
| |
|
|
|
|
|
|
|
|
|
 8 8 |
2922 |
 28 28 |
10227 |
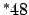 |
17532 |
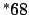 |
24837 |
 88 88 |
32142 |
| 9 |
3288 |
29 |
10593 |
49 |
17898 |
69 |
25203 |
89 |
32508 |
| 10 |
3653 |
30 |
10958 |
50 |
18263 |
70 |
25568 |
90 |
32873 |
| 11 |
4018 |
31 |
11323 |
51 |
18628 |
71 |
25933 |
91 |
33238 |
| |
|
|
|
|
|
|
|
|
|
 12 12 |
4383 |
 32 32 |
11688 |
 52 52 |
18993 |
 72 72 |
26298 |
 92 92 |
33603 |
| 13 |
4749 |
33 |
12054 |
53 |
19359 |
73 |
26664 |
93 |
33969 |
| 14 |
5114 |
34 |
12419 |
54 |
19724 |
74 |
27029 |
94 |
34334 |
| 15 |
5479 |
35 |
12784 |
55 |
20089 |
75 |
27394 |
95 |
34699 |
| |
|
|
|
|
|
|
|
|
|
 16 16 |
5844 |
 36 36 |
13149 |
 56 56 |
20454 |
 76 76 |
27759 |
 96 96 |
35064 |
| 17 |
6210 |
37 |
13515 |
57 |
20820 |
77 |
28125 |
97 |
35430 |
| 18 |
6575 |
38 |
13880 |
58 |
21185 |
78 |
28490 |
98 |
35795 |
| 19 |
6940 |
39 |
14245 |
59 |
21550 |
79 |
28855 |
99 |
36160 |
|
Table 29:
Julian Day Number: Days of the Year.  In leap year,
after February 28, add 1 to the tabulated value. From ``The History
and Practice of Ancient Astronomy", J. Evans (Oxford University Press, Oxford UK, 1998).
In leap year,
after February 28, add 1 to the tabulated value. From ``The History
and Practice of Ancient Astronomy", J. Evans (Oxford University Press, Oxford UK, 1998).
| Day |
Jan |
Feb |
Mar |
Apr |
May |
Jun |
Jul |
Aug |
Sep |
Oct |
Nov |
Dec |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
1 |
32 |
60 |
91 |
121 |
152 |
182 |
213 |
244 |
274 |
305 |
335 |
| 2 |
2 |
33 |
61 |
92 |
122 |
153 |
183 |
214 |
245 |
275 |
306 |
336 |
| 3 |
3 |
34 |
62 |
93 |
123 |
154 |
184 |
215 |
246 |
276 |
307 |
337 |
| 4 |
4 |
35 |
63 |
94 |
124 |
155 |
185 |
216 |
247 |
277 |
308 |
338 |
| 5 |
5 |
36 |
64 |
95 |
125 |
156 |
186 |
217 |
248 |
278 |
309 |
339 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
6 |
37 |
65 |
96 |
126 |
157 |
187 |
218 |
249 |
279 |
310 |
340 |
| 7 |
7 |
38 |
66 |
97 |
127 |
158 |
188 |
219 |
250 |
280 |
311 |
341 |
| 8 |
8 |
39 |
67 |
98 |
128 |
159 |
189 |
220 |
251 |
281 |
312 |
342 |
| 9 |
9 |
40 |
68 |
99 |
129 |
160 |
190 |
221 |
252 |
282 |
313 |
343 |
| 10 |
10 |
41 |
69 |
100 |
130 |
161 |
191 |
222 |
253 |
283 |
314 |
344 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 11 |
11 |
42 |
70 |
101 |
131 |
162 |
192 |
223 |
254 |
284 |
315 |
345 |
| 12 |
12 |
43 |
71 |
102 |
132 |
163 |
193 |
224 |
255 |
285 |
316 |
346 |
| 13 |
13 |
44 |
72 |
103 |
133 |
164 |
194 |
225 |
256 |
286 |
317 |
347 |
| 14 |
14 |
45 |
73 |
104 |
134 |
165 |
195 |
226 |
257 |
285 |
318 |
348 |
| 15 |
15 |
46 |
74 |
105 |
135 |
166 |
196 |
227 |
258 |
288 |
319 |
349 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 16 |
16 |
47 |
75 |
106 |
136 |
167 |
197 |
228 |
259 |
289 |
320 |
350 |
| 17 |
17 |
48 |
76 |
107 |
137 |
168 |
198 |
229 |
260 |
290 |
321 |
351 |
| 18 |
18 |
49 |
77 |
108 |
138 |
169 |
199 |
230 |
261 |
291 |
322 |
352 |
| 19 |
19 |
50 |
78 |
109 |
139 |
170 |
200 |
231 |
262 |
292 |
323 |
353 |
| 20 |
20 |
51 |
79 |
110 |
140 |
171 |
201 |
232 |
263 |
293 |
324 |
354 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 21 |
21 |
52 |
80 |
111 |
141 |
172 |
202 |
233 |
264 |
294 |
325 |
355 |
| 22 |
22 |
53 |
81 |
112 |
142 |
173 |
203 |
234 |
265 |
295 |
326 |
356 |
| 23 |
23 |
54 |
82 |
113 |
143 |
174 |
204 |
235 |
266 |
296 |
327 |
357 |
| 24 |
24 |
55 |
83 |
114 |
144 |
175 |
205 |
236 |
267 |
297 |
328 |
358 |
| 25 |
25 |
56 |
84 |
115 |
145 |
176 |
206 |
237 |
268 |
298 |
329 |
359 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 26 |
26 |
57 |
85 |
116 |
146 |
177 |
207 |
238 |
269 |
299 |
330 |
360 |
| 27 |
27 |
58 |
86 |
117 |
147 |
178 |
208 |
239 |
270 |
300 |
331 |
361 |
| 28 |
28 |
59 |
87 |
118 |
148 |
179 |
209 |
240 |
271 |
301 |
332 |
362 |
| 29 |
29 |
 |
88 |
119 |
149 |
180 |
210 |
241 |
272 |
302 |
333 |
363 |
| 30 |
30 |
|
89 |
120 |
150 |
181 |
211 |
242 |
273 |
303 |
334 |
364 |
| 31 |
31 |
|
90 |
|
151 |
|
212 |
243 |
|
304 |
|
365 |
|


Next: Geometric Planetary Orbit Models
Up: Dates
Previous: Introduction
Richard Fitzpatrick
2010-07-21
![]() JD corresponds to 12:00 UT on June 10, 1992 CE, whereas
JD corresponds to 12:00 UT on June 10, 1992 CE, whereas
![]() JD corresponds to 24:00 UT later the same day.
JD corresponds to 24:00 UT later the same day.