


Next: Determination of Ecliptic Latitude
Up: The Moon
Previous: Determination of Ecliptic Longitude
Example 1: May 5, 2005 CE, 00:00 UT:
From Sect. 5.1, 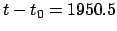 JD,
JD,
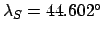 , and
, and
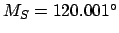 .
Making use of Table 36, we find:
.
Making use of Table 36, we find:
| |
|
|
|
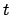 (JD) (JD) |
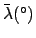 |
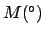 |
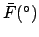 |
| |
|
|
|
| +1000 |
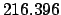 |
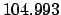 |
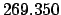 |
| +900 |
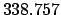 |
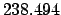 |
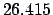 |
| +50 |
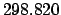 |
 |
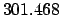 |
| +.5 |
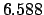 |
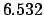 |
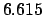 |
| Epoch |
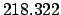 |
 |
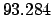 |
| |
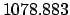 |
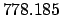 |
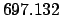 |
| Modulus |
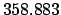 |
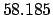 |
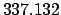 |
| |
|
|
|
It follows that
Thus,
Table 37 yields
Hence,
or
Thus, the ecliptic longitude of the moon at 00:00 UT on May 5, 2005 CE was 3AR05.
Example 2: December 25, 1800 CE, 00:00 UT:
From Sect. 5.1,
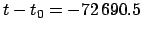 JD,
JD,
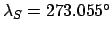 , and
, and
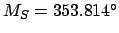 .
Making use of Table 36, we find:
.
Making use of Table 36, we find:
| |
|
|
|
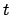 (JD) (JD) |
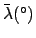 |
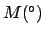 |
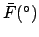 |
| |
|
|
|
| -70,000 |
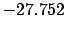 |
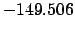 |
 |
| -2,000 |
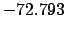 |
 |
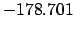 |
| -600 |
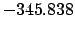 |
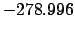 |
 |
| -90 |
 |
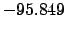 |
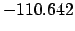 |
| -.5 |
 |
 |
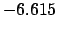 |
| Epoch |
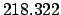 |
 |
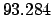 |
| |
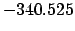 |
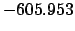 |
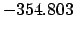 |
| Modulus |
 |
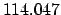 |
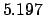 |
| |
|
|
|
It follows that
Thus,
Table 37 yields
Hence,
or
Thus, the ecliptic longitude of the moon at 00:00 UT on December 25, 1800 CE was 25AR57.
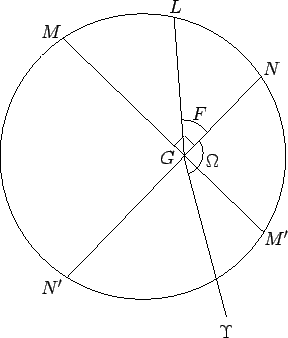
Figure 23:
The orbit of the moon about the earth. Here, 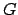 ,
, 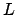 ,
, 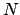 ,
, 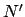 ,
,  ,
, 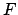 , and
, and 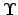 represent the earth, moon, ascending node, descending node, longitude of the ascending node, argument of latitude, and vernal equinox, respectively. View is from northern ecliptic pole. The moon orbits counterclockwise.
represent the earth, moon, ascending node, descending node, longitude of the ascending node, argument of latitude, and vernal equinox, respectively. View is from northern ecliptic pole. The moon orbits counterclockwise.
 |



Next: Determination of Ecliptic Latitude
Up: The Moon
Previous: Determination of Ecliptic Longitude
Richard Fitzpatrick
2010-07-21
![]() JD,
JD,
![]() , and
, and
![]() .
Making use of Table 36, we find:
.
Making use of Table 36, we find:
