

Next: Lunar-Solar Syzygies and Eclipses
Up: The Moon
Previous: Determination of Ecliptic Latitude
Lunar Parallax
Now, it turns out that the moon is sufficiently close to the earth that its position in the sky is
significantly modified by parallax. All of our previous analysis
applies to a hypothetical observer situated at the center of the earth.
Consider a real observer situated on the earth's surface. It can
be seen from Fig. 24 that the altitude of the moon is
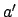 for the real observer, and
for the real observer, and 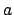 for the hypothetical observer. Simple
trigonometry reveals that
for the hypothetical observer. Simple
trigonometry reveals that
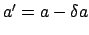 , which implies that the real
observer sees the moon at a lower altitude than the hypothetical observer.
Let
, which implies that the real
observer sees the moon at a lower altitude than the hypothetical observer.
Let 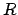 be the radius of the earth, and
be the radius of the earth, and 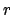 the distance from the center
of the earth to the moon. More simple trigonometry yields
the distance from the center
of the earth to the moon. More simple trigonometry yields
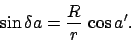 |
(126) |
Let us assume that the moon's orbit is elliptical to first order in its
eccentricity. It follows, from Cha. 4, that
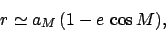 |
(127) |
where 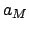 ,
, 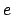 , and
, and 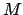 are major radius, eccentricity, and mean
anomaly of the lunar orbit. Assuming that
are major radius, eccentricity, and mean
anomaly of the lunar orbit. Assuming that 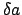 is small, we
obtain
is small, we
obtain
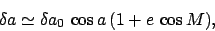 |
(128) |
where
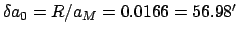 (since
(since 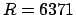 km and
km and 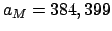 km).
km).
According to Eq. (128), lunar parallax can be written in the form
![\begin{displaymath}
\delta a = \delta (a)\,[1+\zeta (M)],
\end{displaymath}](img1334.png) |
(129) |
where 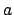 ,
, 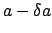 , and
, and 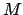 are the moon's geocentric altitude (i.e., the altitude seen from the center of the earth), true
altitude, and mean anomaly, respectively. The functions
are the moon's geocentric altitude (i.e., the altitude seen from the center of the earth), true
altitude, and mean anomaly, respectively. The functions
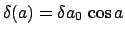 and
and
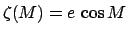 are tabulated in Table 39. It can be seen from the
table that lunar parallax increases with decreasing lunar altitude, reaching a maximum value of about
are tabulated in Table 39. It can be seen from the
table that lunar parallax increases with decreasing lunar altitude, reaching a maximum value of about 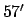 when the moon is close to the horizon.
For example, if
when the moon is close to the horizon.
For example, if
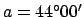 and
and 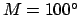 then Table 39
yields
then Table 39
yields
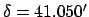 and
and
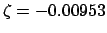 . Hence,
. Hence,
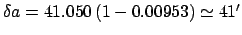 , and the true altitude of the moon becomes
, and the true altitude of the moon becomes
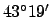 .
.
Figure 25:
Parallactic shifts in the moon's ecliptic longitude and latitude.
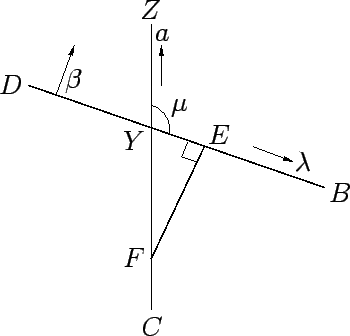 |
It now remains to investigate how parallax affects the moon's ecliptic
longitude and latitude. Figure 25 shows a detail of Fig. 13. Point 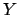 is the moon's geocentric position on the celestial sphere.
is the moon's geocentric position on the celestial sphere. 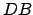 is a line passing through this point
which is parallel to the local ecliptic circle, whereas
is a line passing through this point
which is parallel to the local ecliptic circle, whereas 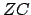 is a small section of an
altitude circle passing through
is a small section of an
altitude circle passing through 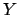 . The angle subtended between the ecliptic and the altitude circle is the parallactic angle,
. The angle subtended between the ecliptic and the altitude circle is the parallactic angle, 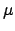 . Let
. Let 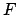 be the true position of the moon.
It follows that
be the true position of the moon.
It follows that 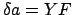 . The changes in the moon's ecliptic longitude
and latitude are
. The changes in the moon's ecliptic longitude
and latitude are
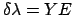 and
and
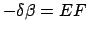 , respectively. Here, we are considering the case where increasing
altitude corresponds to increasing ecliptic latitude.
Assuming that the arcs
, respectively. Here, we are considering the case where increasing
altitude corresponds to increasing ecliptic latitude.
Assuming that the arcs 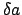 ,
, 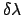 , and
, and 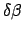 are
all fairly small, the triangle
are
all fairly small, the triangle 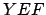 can be treated as a plane triangle.
Hence, we obtain
can be treated as a plane triangle.
Hence, we obtain
As is easily demonstrated, the above formulae also apply to the case in which increasing altitude corresponds
to decreasing ecliptic latitude.
For example, consider a day on which the geocentric ecliptic longitude and mean anomaly
of the moon are
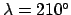 (i.e., 00SC00) and
(i.e., 00SC00) and 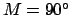 , respectively. Suppose that the moon is
viewed from an observation site located at terrestrial latitude
, respectively. Suppose that the moon is
viewed from an observation site located at terrestrial latitude 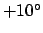 .
The ``Scorpio'' entry in Table 19 gives the moon's geocentric altitude,
.
The ``Scorpio'' entry in Table 19 gives the moon's geocentric altitude, 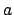 , as a function of time, as well as the
value of the parallactic angle
, as a function of time, as well as the
value of the parallactic angle 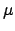 . Making use of this data,
in combination with Table 39 and Eqs. (130) and (131), we can calculate the parallax-induced changes in the moon's ecliptic
longitude and latitude as it transits the sky.
Data from such a calculation is given in the table below. The first column specifies
time since the moon's upper transit (thus,
. Making use of this data,
in combination with Table 39 and Eqs. (130) and (131), we can calculate the parallax-induced changes in the moon's ecliptic
longitude and latitude as it transits the sky.
Data from such a calculation is given in the table below. The first column specifies
time since the moon's upper transit (thus, 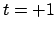 hrs. means one hour after the
upper transit), the second column gives the moon's geocentric altitude, the third column the parallactic angle,
the
fourth column the decrease in the moon's real altitude due to parallax, and the fifth and
sixth columns the parallax-induced changes in its ecliptic longitude and latitude, respectively.
It can be seen that parallax causes the moon's apparent location
to shift by almost
hrs. means one hour after the
upper transit), the second column gives the moon's geocentric altitude, the third column the parallactic angle,
the
fourth column the decrease in the moon's real altitude due to parallax, and the fifth and
sixth columns the parallax-induced changes in its ecliptic longitude and latitude, respectively.
It can be seen that parallax causes the moon's apparent location
to shift by almost 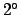 relative to the fixed stars as it transits the sky. Note that the
above calculation is somewhat inaccurate because it does not take into account the moon's motion along the
ecliptic (which can easily amount to
relative to the fixed stars as it transits the sky. Note that the
above calculation is somewhat inaccurate because it does not take into account the moon's motion along the
ecliptic (which can easily amount to 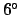 during the course of a night).
However, the calculation does illustrate how the data contained in
Tables 18-26, in combination with the data in Table 39, permits the parallax-induced shift in the moon's ecliptic position
to be calculated for a wide range of different lunar phases,
observation sites, and observation times.
during the course of a night).
However, the calculation does illustrate how the data contained in
Tables 18-26, in combination with the data in Table 39, permits the parallax-induced shift in the moon's ecliptic position
to be calculated for a wide range of different lunar phases,
observation sites, and observation times.
Table 35:
Orbital elements of the moon for the J2000 epoch (i.e., 12:00 UT, January 1, 2000 CE,
which corresponds to
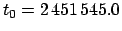 JD).
JD).
 |
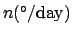 |
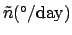 |
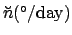 |
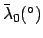 |
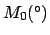 |
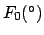 |
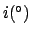 |
| 0.054881 |
13.17639646 |
13.06499295 |
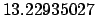 |
218.322 |
134.916 |
93.284 |
5.161 |
|
Table 36:
Mean motion of the moon. Here,
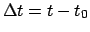 ,
,
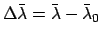 ,
,
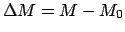 , and
, and
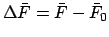 .
At epoch (
.
At epoch (
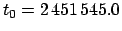 JD),
JD),
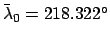 ,
,
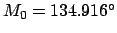 ,
and
,
and
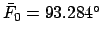 .
.
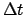 (JD) (JD) |
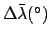 |
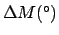 |
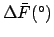 |
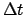 (JD) (JD) |
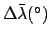 |
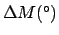 |
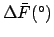 |
| |
|
|
|
|
|
|
|
| 10,000 |
3.965 |
329.930 |
173.503 |
1,000 |
216.396 |
104.993 |
269.350 |
| 20,000 |
7.929 |
299.859 |
347.005 |
2,000 |
72.793 |
209.986 |
178.701 |
| 30,000 |
11.894 |
269.788 |
160.508 |
3,000 |
289.189 |
314.979 |
88.051 |
| 40,000 |
15.858 |
239.718 |
334.011 |
4,000 |
145.586 |
59.972 |
357.401 |
| 50,000 |
19.823 |
209.648 |
147.513 |
5,000 |
1.982 |
164.965 |
266.751 |
| 60,000 |
23.788 |
179.577 |
321.016 |
6,000 |
218.379 |
269.958 |
176.102 |
| 70,000 |
27.752 |
149.506 |
134.519 |
7,000 |
74.775 |
14.951 |
85.452 |
| 80,000 |
31.717 |
119.436 |
308.022 |
8,000 |
291.172 |
119.944 |
354.802 |
| 90,000 |
35.681 |
89.366 |
121.524 |
9,000 |
147.568 |
224.937 |
264.152 |
| |
|
|
|
|
|
|
|
| 100 |
237.640 |
226.499 |
242.935 |
10 |
131.764 |
130.650 |
132.294 |
| 200 |
115.279 |
92.999 |
125.870 |
20 |
263.528 |
261.300 |
264.587 |
| 300 |
352.919 |
319.498 |
8.805 |
30 |
35.292 |
31.950 |
36.881 |
| 400 |
230.559 |
185.997 |
251.740 |
40 |
167.056 |
162.600 |
169.174 |
| 500 |
108.198 |
52.496 |
134.675 |
50 |
298.820 |
293.250 |
301.468 |
| 600 |
345.838 |
278.996 |
17.610 |
60 |
70.584 |
63.900 |
73.761 |
| 700 |
223.478 |
145.495 |
260.545 |
70 |
202.348 |
194.550 |
206.055 |
| 800 |
101.117 |
11.994 |
143.480 |
80 |
334.112 |
325.199 |
338.348 |
| 900 |
338.757 |
238.494 |
26.415 |
90 |
105.876 |
95.849 |
110.642 |
| |
|
|
|
|
|
|
|
| 1 |
13.176 |
13.065 |
13.229 |
0.1 |
1.318 |
1.306 |
1.323 |
| 2 |
26.353 |
26.130 |
26.459 |
0.2 |
2.635 |
2.613 |
2.646 |
| 3 |
39.529 |
39.195 |
39.688 |
0.3 |
3.953 |
3.919 |
3.969 |
| 4 |
52.706 |
52.260 |
52.917 |
0.4 |
5.271 |
5.226 |
5.292 |
| 5 |
65.882 |
65.325 |
66.147 |
0.5 |
6.588 |
6.532 |
6.615 |
| 6 |
79.058 |
78.390 |
79.376 |
0.6 |
7.906 |
7.839 |
7.938 |
| 7 |
92.235 |
91.455 |
92.605 |
0.7 |
9.223 |
9.145 |
9.261 |
| 8 |
105.411 |
104.520 |
105.835 |
0.8 |
10.541 |
10.452 |
10.583 |
| 9 |
118.588 |
117.585 |
119.064 |
0.9 |
11.859 |
11.758 |
11.906 |
|
Table 37:
Anomalies of the moon. The common argument corresponds to
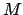 ,
, 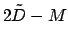 ,
, 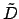 ,
, 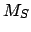 , and
, and 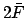 for the case of
for the case of
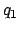 ,
, 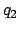 ,
, 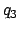 ,
, 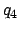 , and
, and 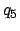 , respectively. If the argument is
in parenthesies then the anomalies are minus the values shown
in the table.
, respectively. If the argument is
in parenthesies then the anomalies are minus the values shown
in the table.
Arg. (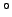 ) ) |
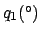 |
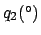 |
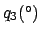 |
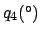 |
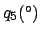 |
Arg. (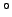 ) ) |
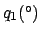 |
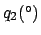 |
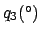 |
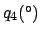 |
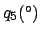 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
000/(360) |
0.000 |
0.000 |
0.000 |
-0.000 |
-0.000 |
090/(270) |
6.289 |
1.327 |
-0.044 |
-0.160 |
-0.119 |
|
002/(358) |
0.237 |
0.046 |
0.045 |
-0.006 |
-0.004 |
092/(268) |
6.268 |
1.326 |
-0.090 |
-0.160 |
-0.119 |
|
004/(356) |
0.473 |
0.093 |
0.089 |
-0.011 |
-0.008 |
094/(266) |
6.239 |
1.324 |
-0.136 |
-0.160 |
-0.119 |
|
006/(354) |
0.709 |
0.139 |
0.133 |
-0.017 |
-0.012 |
096/(264) |
6.203 |
1.320 |
-0.182 |
-0.159 |
-0.119 |
|
008/(352) |
0.943 |
0.185 |
0.177 |
-0.022 |
-0.017 |
098/(262) |
6.160 |
1.314 |
-0.226 |
-0.159 |
-0.118 |
|
010/(350) |
1.176 |
0.230 |
0.219 |
-0.028 |
-0.021 |
100/(260) |
6.109 |
1.307 |
-0.270 |
-0.158 |
-0.118 |
|
012/(348) |
1.408 |
0.276 |
0.261 |
-0.033 |
-0.025 |
102/(258) |
6.051 |
1.298 |
-0.313 |
-0.157 |
-0.117 |
|
014/(346) |
1.637 |
0.321 |
0.301 |
-0.039 |
-0.029 |
104/(256) |
5.986 |
1.288 |
-0.354 |
-0.156 |
-0.116 |
|
016/(344) |
1.864 |
0.366 |
0.339 |
-0.044 |
-0.033 |
106/(254) |
5.915 |
1.276 |
-0.394 |
-0.154 |
-0.115 |
|
018/(342) |
2.088 |
0.410 |
0.376 |
-0.050 |
-0.037 |
108/(252) |
5.836 |
1.262 |
-0.432 |
-0.153 |
-0.114 |
|
020/(340) |
2.310 |
0.454 |
0.411 |
-0.055 |
-0.041 |
110/(250) |
5.751 |
1.247 |
-0.468 |
-0.151 |
-0.112 |
|
022/(338) |
2.527 |
0.497 |
0.444 |
-0.060 |
-0.045 |
112/(248) |
5.660 |
1.230 |
-0.502 |
-0.149 |
-0.111 |
|
024/(336) |
2.741 |
0.540 |
0.475 |
-0.065 |
-0.049 |
114/(246) |
5.562 |
1.212 |
-0.533 |
-0.147 |
-0.109 |
|
026/(334) |
2.951 |
0.582 |
0.504 |
-0.070 |
-0.052 |
116/(244) |
5.458 |
1.193 |
-0.562 |
-0.144 |
-0.107 |
|
028/(332) |
3.157 |
0.623 |
0.529 |
-0.075 |
-0.056 |
118/(242) |
5.348 |
1.172 |
-0.589 |
-0.142 |
-0.106 |
|
030/(330) |
3.358 |
0.663 |
0.553 |
-0.080 |
-0.060 |
120/(240) |
5.233 |
1.149 |
-0.613 |
-0.139 |
-0.103 |
|
032/(328) |
3.554 |
0.703 |
0.573 |
-0.085 |
-0.063 |
122/(238) |
5.111 |
1.125 |
-0.634 |
-0.136 |
-0.101 |
|
034/(326) |
3.746 |
0.742 |
0.591 |
-0.090 |
-0.067 |
124/(236) |
4.985 |
1.100 |
-0.652 |
-0.133 |
-0.099 |
|
036/(324) |
3.931 |
0.780 |
0.605 |
-0.094 |
-0.070 |
126/(234) |
4.853 |
1.074 |
-0.667 |
-0.130 |
-0.097 |
|
038/(322) |
4.111 |
0.817 |
0.617 |
-0.099 |
-0.074 |
128/(232) |
4.716 |
1.046 |
-0.678 |
-0.126 |
-0.094 |
|
040/(320) |
4.285 |
0.853 |
0.625 |
-0.103 |
-0.077 |
130/(230) |
4.575 |
1.017 |
-0.687 |
-0.123 |
-0.092 |
|
042/(318) |
4.454 |
0.888 |
0.630 |
-0.107 |
-0.080 |
132/(228) |
4.428 |
0.986 |
-0.693 |
-0.119 |
-0.089 |
|
044/(316) |
4.615 |
0.922 |
0.632 |
-0.111 |
-0.083 |
134/(226) |
4.277 |
0.955 |
-0.695 |
-0.115 |
-0.086 |
|
046/(314) |
4.770 |
0.955 |
0.631 |
-0.115 |
-0.086 |
136/(224) |
4.122 |
0.922 |
-0.694 |
-0.111 |
-0.083 |
|
048/(312) |
4.919 |
0.986 |
0.627 |
-0.119 |
-0.089 |
138/(222) |
3.963 |
0.888 |
-0.689 |
-0.107 |
-0.080 |
|
050/(310) |
5.061 |
1.017 |
0.620 |
-0.123 |
-0.092 |
140/(220) |
3.799 |
0.853 |
-0.682 |
-0.103 |
-0.077 |
|
052/(308) |
5.195 |
1.046 |
0.609 |
-0.126 |
-0.094 |
142/(218) |
3.632 |
0.817 |
-0.671 |
-0.099 |
-0.074 |
|
054/(306) |
5.323 |
1.074 |
0.595 |
-0.130 |
-0.097 |
144/(216) |
3.462 |
0.780 |
-0.657 |
-0.094 |
-0.070 |
|
056/(304) |
5.443 |
1.100 |
0.579 |
-0.133 |
-0.099 |
146/(214) |
3.288 |
0.742 |
-0.640 |
-0.090 |
-0.067 |
|
058/(302) |
5.555 |
1.125 |
0.559 |
-0.136 |
-0.101 |
148/(212) |
3.111 |
0.703 |
-0.620 |
-0.085 |
-0.063 |
|
060/(300) |
5.660 |
1.149 |
0.536 |
-0.139 |
-0.103 |
150/(210) |
2.931 |
0.663 |
-0.597 |
-0.080 |
-0.060 |
|
062/(298) |
5.757 |
1.172 |
0.511 |
-0.142 |
-0.106 |
152/(208) |
2.748 |
0.623 |
-0.571 |
-0.075 |
-0.056 |
|
064/(296) |
5.847 |
1.193 |
0.483 |
-0.144 |
-0.107 |
154/(206) |
2.562 |
0.582 |
-0.542 |
-0.070 |
-0.052 |
|
066/(294) |
5.929 |
1.212 |
0.453 |
-0.147 |
-0.109 |
156/(204) |
2.375 |
0.540 |
-0.511 |
-0.065 |
-0.049 |
|
068/(292) |
6.002 |
1.230 |
0.420 |
-0.149 |
-0.111 |
158/(202) |
2.184 |
0.497 |
-0.477 |
-0.060 |
-0.045 |
|
070/(290) |
6.068 |
1.247 |
0.385 |
-0.151 |
-0.112 |
160/(200) |
1.992 |
0.454 |
-0.442 |
-0.055 |
-0.041 |
|
072/(288) |
6.126 |
1.262 |
0.348 |
-0.153 |
-0.114 |
162/(198) |
1.798 |
0.410 |
-0.404 |
-0.050 |
-0.037 |
|
074/(286) |
6.176 |
1.276 |
0.309 |
-0.154 |
-0.115 |
164/(196) |
1.603 |
0.366 |
-0.364 |
-0.044 |
-0.033 |
|
076/(284) |
6.218 |
1.288 |
0.269 |
-0.156 |
-0.116 |
166/(194) |
1.406 |
0.321 |
-0.322 |
-0.039 |
-0.029 |
|
078/(282) |
6.252 |
1.298 |
0.227 |
-0.157 |
-0.117 |
168/(192) |
1.207 |
0.276 |
-0.279 |
-0.033 |
-0.025 |
|
080/(280) |
6.278 |
1.307 |
0.184 |
-0.158 |
-0.118 |
170/(190) |
1.008 |
0.230 |
-0.235 |
-0.028 |
-0.021 |
|
082/(278) |
6.296 |
1.314 |
0.139 |
-0.159 |
-0.118 |
172/(188) |
0.807 |
0.185 |
-0.189 |
-0.022 |
-0.017 |
|
084/(276) |
6.306 |
1.320 |
0.094 |
-0.159 |
-0.119 |
174/(186) |
0.606 |
0.139 |
-0.143 |
-0.017 |
-0.012 |
|
086/(274) |
6.308 |
1.324 |
0.048 |
-0.160 |
-0.119 |
176/(184) |
0.404 |
0.093 |
-0.095 |
-0.011 |
-0.008 |
|
088/(272) |
6.302 |
1.326 |
0.002 |
-0.160 |
-0.119 |
178/(182) |
0.202 |
0.046 |
-0.048 |
-0.006 |
-0.004 |
|
090/(270) |
6.289 |
1.327 |
-0.044 |
-0.160 |
-0.119 |
180/(180) |
0.000 |
0.000 |
-0.000 |
-0.000 |
-0.000 |
|
Table 38:
Ecliptic latitude of the moon. The latitude is minus the value shown
in the table if the argument is
in parenthesies.
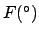 |
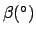 |
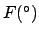 |
|
|
|
|
|
000/180 |
0.000 |
(180)/(360) |
|
002/178 |
0.180 |
(182)/(358) |
|
004/176 |
0.360 |
(184)/(356) |
|
006/174 |
0.539 |
(186)/(354) |
|
008/172 |
0.718 |
(188)/(352) |
|
010/170 |
0.896 |
(190)/(350) |
|
012/168 |
1.073 |
(192)/(348) |
|
014/166 |
1.248 |
(194)/(346) |
|
016/164 |
1.422 |
(196)/(344) |
|
018/162 |
1.595 |
(198)/(342) |
|
020/160 |
1.765 |
(200)/(340) |
|
022/158 |
1.933 |
(202)/(338) |
|
024/156 |
2.099 |
(204)/(336) |
|
026/154 |
2.263 |
(206)/(334) |
|
028/152 |
2.423 |
(208)/(332) |
|
030/150 |
2.581 |
(210)/(330) |
|
032/148 |
2.735 |
(212)/(328) |
|
034/146 |
2.887 |
(214)/(326) |
|
036/144 |
3.034 |
(216)/(324) |
|
038/142 |
3.178 |
(218)/(322) |
|
040/140 |
3.319 |
(220)/(320) |
|
042/138 |
3.455 |
(222)/(318) |
|
044/136 |
3.587 |
(224)/(316) |
|
046/134 |
3.714 |
(226)/(314) |
|
048/132 |
3.837 |
(228)/(312) |
|
050/130 |
3.956 |
(230)/(310) |
|
052/128 |
4.070 |
(232)/(308) |
|
054/126 |
4.178 |
(234)/(306) |
|
056/124 |
4.282 |
(236)/(304) |
|
058/122 |
4.380 |
(238)/(302) |
|
060/120 |
4.473 |
(240)/(300) |
|
062/118 |
4.561 |
(242)/(298) |
|
064/116 |
4.643 |
(244)/(296) |
|
066/114 |
4.719 |
(246)/(294) |
|
068/112 |
4.790 |
(248)/(292) |
|
070/110 |
4.855 |
(250)/(290) |
|
072/108 |
4.913 |
(252)/(288) |
|
074/106 |
4.966 |
(254)/(286) |
|
076/104 |
5.013 |
(256)/(284) |
|
078/102 |
5.054 |
(258)/(282) |
|
080/100 |
5.088 |
(260)/(280) |
|
082/098 |
5.117 |
(262)/(278) |
|
084/096 |
5.139 |
(264)/(276) |
|
086/094 |
5.154 |
(266)/(274) |
|
088/092 |
5.164 |
(268)/(272) |
|
090/090 |
5.167 |
(270)/(270) |
|
Table 39:
Parallax of the moon. The arguments of 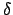 and
and 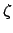 are
are 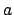 and
and 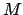 , respectively.
, respectively. 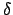 and
and 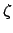 take minus the values shown
in the table if their arguments are
in parenthesies.
take minus the values shown
in the table if their arguments are
in parenthesies.
Arg. (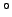 ) ) |
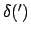 |
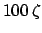 |
Arg. (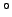 ) ) |
|
|
|
|
|
|
000/360 |
57.067 |
5.488 |
(180)/(180) |
|
002/358 |
57.032 |
5.485 |
(178)/(182) |
|
004/356 |
56.928 |
5.475 |
(176)/(184) |
|
006/354 |
56.754 |
5.458 |
(174)/(186) |
|
008/352 |
56.511 |
5.435 |
(172)/(188) |
|
010/350 |
56.200 |
5.405 |
(170)/(190) |
|
012/348 |
55.820 |
5.368 |
(168)/(192) |
|
014/346 |
55.371 |
5.325 |
(166)/(194) |
|
016/344 |
54.856 |
5.276 |
(164)/(196) |
|
018/342 |
54.274 |
5.219 |
(162)/(198) |
|
020/340 |
53.625 |
5.157 |
(160)/(200) |
|
022/338 |
52.911 |
5.088 |
(158)/(202) |
|
024/336 |
52.133 |
5.014 |
(156)/(204) |
|
026/334 |
51.291 |
4.933 |
(154)/(206) |
|
028/332 |
50.387 |
4.846 |
(152)/(208) |
|
030/330 |
49.421 |
4.753 |
(150)/(210) |
|
032/328 |
48.395 |
4.654 |
(148)/(212) |
|
034/326 |
47.310 |
4.550 |
(146)/(214) |
|
036/324 |
46.168 |
4.440 |
(144)/(216) |
|
038/322 |
44.969 |
4.325 |
(142)/(218) |
|
040/320 |
43.716 |
4.204 |
(140)/(220) |
|
042/318 |
42.409 |
4.078 |
(138)/(222) |
|
044/316 |
41.050 |
3.948 |
(136)/(224) |
|
046/314 |
39.642 |
3.812 |
(134)/(226) |
|
048/312 |
38.185 |
3.672 |
(132)/(228) |
|
050/310 |
36.682 |
3.528 |
(130)/(230) |
|
052/308 |
35.134 |
3.379 |
(128)/(232) |
|
054/306 |
33.543 |
3.226 |
(126)/(234) |
|
056/304 |
31.911 |
3.069 |
(124)/(236) |
|
058/302 |
30.241 |
2.908 |
(122)/(238) |
|
060/300 |
28.533 |
2.744 |
(120)/(240) |
|
062/298 |
26.791 |
2.577 |
(118)/(242) |
|
064/296 |
25.016 |
2.406 |
(116)/(244) |
|
066/294 |
23.211 |
2.232 |
(114)/(246) |
|
068/292 |
21.378 |
2.056 |
(112)/(248) |
|
070/290 |
19.518 |
1.877 |
(110)/(250) |
|
072/288 |
17.635 |
1.696 |
(108)/(252) |
|
074/286 |
15.730 |
1.513 |
(106)/(254) |
|
076/284 |
13.806 |
1.328 |
(104)/(256) |
|
078/282 |
11.865 |
1.141 |
(102)/(258) |
|
080/280 |
9.910 |
0.953 |
(100)/(260) |
|
082/278 |
7.942 |
0.764 |
(098)/(262) |
|
084/276 |
5.965 |
0.574 |
(096)/(264) |
|
086/274 |
3.981 |
0.383 |
(094)/(266) |
|
088/272 |
1.992 |
0.192 |
(092)/(268) |
|
090/270 |
0.000 |
0.000 |
(090)/(270) |
|


Next: Lunar-Solar Syzygies and Eclipses
Up: The Moon
Previous: Determination of Ecliptic Latitude
Richard Fitzpatrick
2010-07-21
![]() is the moon's geocentric position on the celestial sphere.
is the moon's geocentric position on the celestial sphere. ![]() is a line passing through this point
which is parallel to the local ecliptic circle, whereas
is a line passing through this point
which is parallel to the local ecliptic circle, whereas ![]() is a small section of an
altitude circle passing through
is a small section of an
altitude circle passing through ![]() . The angle subtended between the ecliptic and the altitude circle is the parallactic angle,
. The angle subtended between the ecliptic and the altitude circle is the parallactic angle, ![]() . Let
. Let ![]() be the true position of the moon.
It follows that
be the true position of the moon.
It follows that ![]() . The changes in the moon's ecliptic longitude
and latitude are
. The changes in the moon's ecliptic longitude
and latitude are
![]() and
and
![]() , respectively. Here, we are considering the case where increasing
altitude corresponds to increasing ecliptic latitude.
Assuming that the arcs
, respectively. Here, we are considering the case where increasing
altitude corresponds to increasing ecliptic latitude.
Assuming that the arcs ![]() ,
, ![]() , and
, and ![]() are
all fairly small, the triangle
are
all fairly small, the triangle ![]() can be treated as a plane triangle.
Hence, we obtain
can be treated as a plane triangle.
Hence, we obtain
![]() (i.e., 00SC00) and
(i.e., 00SC00) and ![]() , respectively. Suppose that the moon is
viewed from an observation site located at terrestrial latitude
, respectively. Suppose that the moon is
viewed from an observation site located at terrestrial latitude ![]() .
The ``Scorpio'' entry in Table 19 gives the moon's geocentric altitude,
.
The ``Scorpio'' entry in Table 19 gives the moon's geocentric altitude, ![]() , as a function of time, as well as the
value of the parallactic angle
, as a function of time, as well as the
value of the parallactic angle ![]() . Making use of this data,
in combination with Table 39 and Eqs. (130) and (131), we can calculate the parallax-induced changes in the moon's ecliptic
longitude and latitude as it transits the sky.
Data from such a calculation is given in the table below. The first column specifies
time since the moon's upper transit (thus,
. Making use of this data,
in combination with Table 39 and Eqs. (130) and (131), we can calculate the parallax-induced changes in the moon's ecliptic
longitude and latitude as it transits the sky.
Data from such a calculation is given in the table below. The first column specifies
time since the moon's upper transit (thus, ![]() hrs. means one hour after the
upper transit), the second column gives the moon's geocentric altitude, the third column the parallactic angle,
the
fourth column the decrease in the moon's real altitude due to parallax, and the fifth and
sixth columns the parallax-induced changes in its ecliptic longitude and latitude, respectively.
It can be seen that parallax causes the moon's apparent location
to shift by almost
hrs. means one hour after the
upper transit), the second column gives the moon's geocentric altitude, the third column the parallactic angle,
the
fourth column the decrease in the moon's real altitude due to parallax, and the fifth and
sixth columns the parallax-induced changes in its ecliptic longitude and latitude, respectively.
It can be seen that parallax causes the moon's apparent location
to shift by almost ![]() relative to the fixed stars as it transits the sky. Note that the
above calculation is somewhat inaccurate because it does not take into account the moon's motion along the
ecliptic (which can easily amount to
relative to the fixed stars as it transits the sky. Note that the
above calculation is somewhat inaccurate because it does not take into account the moon's motion along the
ecliptic (which can easily amount to ![]() during the course of a night).
However, the calculation does illustrate how the data contained in
Tables 18-26, in combination with the data in Table 39, permits the parallax-induced shift in the moon's ecliptic position
to be calculated for a wide range of different lunar phases,
observation sites, and observation times.
during the course of a night).
However, the calculation does illustrate how the data contained in
Tables 18-26, in combination with the data in Table 39, permits the parallax-induced shift in the moon's ecliptic position
to be calculated for a wide range of different lunar phases,
observation sites, and observation times.