


Next: Ecliptic Altitude and Orientation
Up: Spherical Astronomy
Previous: Ecliptic Ascensions
Consider the azimuth of the point on the ecliptic circle which is ascending at the
eastern horizon.
According to Eq. (27), the azimuth of any point on the horizon (i.e., 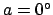 ) satisfies
) satisfies
 . It
follows from Eqs. (8) and (25) that
. It
follows from Eqs. (8) and (25) that
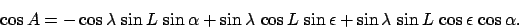 |
(42) |
Here, we have made use of the fact that the point in question also lies on the
ecliptic (i.e., 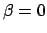 ), as well as the fact that
), as well as the fact that
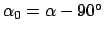 ,
where
,
where 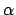 is the right ascension of the simultaneously rising point on the celestial
equator. Here,
is the right ascension of the simultaneously rising point on the celestial
equator. Here, 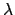 is the ecliptic longitude of the point in question, and
is the ecliptic longitude of the point in question, and 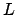 the terrestrial latitude of the observation
site.
Now,
the terrestrial latitude of the observation
site.
Now, 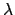 and
and 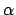 satisfy Eq. (39), as well as the above equation. Thus,
eliminating
satisfy Eq. (39), as well as the above equation. Thus,
eliminating 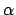 between these two equations, we obtain
between these two equations, we obtain
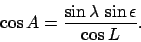 |
(43) |
This expression gives the azimuth, 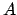 , of the ascending point of the ecliptic as a function of
its ecliptic longitude,
, of the ascending point of the ecliptic as a function of
its ecliptic longitude, 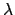 , and the latitude,
, and the latitude, 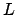 , of the
observation site.
, of the
observation site.
For instance, suppose that we wish to find the azimuth of the point at which the sun rises on
the eastern horizon at an observation site of terrestrial latitude  , on a day on which the sun's ecliptic longitude is 08PI00. It
follows from Eq. (43) that
, on a day on which the sun's ecliptic longitude is 08PI00. It
follows from Eq. (43) that
![$A= \cos^{-1}[\sin (338^\circ)\,\sin (23^\circ 26')/\cos (60^\circ)] = 107^\circ 20'$](img274.png) . We conclude that the
sun rises
. We conclude that the
sun rises  to the south of the east compass point on the
day in question. It is easily demonstrated that the sun sets
to the south of the east compass point on the
day in question. It is easily demonstrated that the sun sets  south of the west compass point
on the same day (neglecting the slight change in the sun's ecliptic latitude during the course of the day.)
Likewise, it can easily be shown that, at an observation site of terrestrial latitude
south of the west compass point
on the same day (neglecting the slight change in the sun's ecliptic latitude during the course of the day.)
Likewise, it can easily be shown that, at an observation site of terrestrial latitude 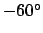 , the
sun also rises
, the
sun also rises  to the south of the east compass point on the day in question, and sets
to the south of the east compass point on the day in question, and sets  to the south of
the west compass point.
to the south of
the west compass point.



Next: Ecliptic Altitude and Orientation
Up: Spherical Astronomy
Previous: Ecliptic Ascensions
Richard Fitzpatrick
2010-07-21
![]() , on a day on which the sun's ecliptic longitude is 08PI00. It
follows from Eq. (43) that
, on a day on which the sun's ecliptic longitude is 08PI00. It
follows from Eq. (43) that
![]() . We conclude that the
sun rises
. We conclude that the
sun rises ![]() to the south of the east compass point on the
day in question. It is easily demonstrated that the sun sets
to the south of the east compass point on the
day in question. It is easily demonstrated that the sun sets ![]() south of the west compass point
on the same day (neglecting the slight change in the sun's ecliptic latitude during the course of the day.)
Likewise, it can easily be shown that, at an observation site of terrestrial latitude
south of the west compass point
on the same day (neglecting the slight change in the sun's ecliptic latitude during the course of the day.)
Likewise, it can easily be shown that, at an observation site of terrestrial latitude ![]() , the
sun also rises
, the
sun also rises ![]() to the south of the east compass point on the day in question, and sets
to the south of the east compass point on the day in question, and sets ![]() to the south of
the west compass point.
to the south of
the west compass point.