Local Horizon and Meridian

Consider a general observation site $X$ on the surface of the earth. (Note that, in the following, it is tacitly assumed that the site lies the earth's northern hemisphere. However, the analysis also applies to sites situated in the the southern hemisphere.) The local zenith $Z$ is the point on the celestial sphere which is directly overhead at $X$, whereas the nadir $Z'$ is the point which is directly underfoot--see Fig. 7. The horizon is the tangent plane to the earth at $X$, and divides the celestial sphere into two halves. The upper half, containing the zenith, is visible from site $X$, whereas the lower half is invisible.

Figure 7: A general observation site $X$, of latitude $L$, on the surface of the earth. $P$, $P'$, $Z$, and $Z'$ denote the directions to the north celestial pole, south celestial pole, zenith, and nadir, respectively. The line $NS$ represents the local horizon.

Figure 8: The local horizon and meridian. $N$, $S$, $E$, $W$ denote the north. south, east, and west compass points, $Z$ the zenith, and $P$ the north celestial pole. $NESW$ is the horizon, and $NPZS$ the meridian.

Figure 8 shows the visible half of the celestial sphere at observation site $X$. Here, $NESW$ is the local horizon, and $N$, $E$, $S$, and $W$ are the north, east, south, and west compass points, respectively. The plane $NPZS$, which passes through the north and south compass points, as well as the zenith, is known as the local meridian. The meridian is perpendicular to the horizon. The north celestial pole lies in the meridian plane, and is elevated an angular distance $L$ above the north compass point--see Figs. 7 and 8. Here, $L$ is the terrestrial latitude of observation site $X$. It is helpful to define three, right-handed, mutually perpendicular, local unit vectors: ${\bf e}$, ${\bf n}$, and ${\bf z}$. Here, ${\bf e}$ is directed toward the east compass point, ${\bf n}$ toward the north compass point, and ${\bf z}$ toward the zenith--see Fig. 8.

Figure 9: The local meridian.

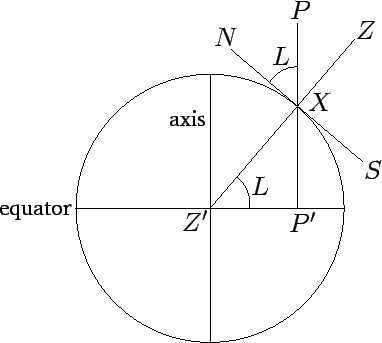
Figure 9 shows the meridian plane at $X$. Let the line $MM'$ lie in this plane such that it is perpendicular to the celestial axis, $PP'$. Moreover, let $M$ lie in the visible hemisphere. It is helpful to define the unit vector ${\bf m}$ which is directed toward $M$, as shown in the diagram. It is easily seen that

$${\bf n} = \cos L\,{\bf p} - \sin L\,{\bf m},$$ (17)

$${\bf z} = \sin L\,{\bf p} + \cos L\,{\bf m}.$$ (18)

Figure 10: The local celestial equator.

Figure 10 shows the celestial equator viewed from observation site $X$. Here, $\alpha_0$ is the right ascension of the celestial objects culminating (i.e., reaching their highest altitude in the sky) on the meridian at the time of observation. Incidentally, it is easily demonstrated that all objects culminating on the meridian at any instant in time have the same right ascension. Note that the angle $\alpha_0$ increases uniformly in time, at the rate of $15^\circ$ a (sidereal) hour, due to the diurnal motion of the celestial sphere. It can be seen from the diagram that

$${\bf m} = \sin \alpha_0\,{\bf u} + \cos \alpha_0\,{\bf v},$$ (19)

$${\bf e} = \cos \alpha_0 \,{\bf u} -\sin \alpha_0\,{\bf v}.$$ (20)

Thus, from Eqs. (17) and (18),

$${\bf e} = -\sin \alpha_0\,{\bf v} + \cos \alpha_0\,{\bf u},$$ (21)

$${\bf n} = -\sin L\,\cos \alpha_0\,{\bf v} - \sin L\,\sin \alpha_0\,{\bf u} + \cos L\,{\bf p},$$ (22)

$${\bf z} = \cos L\,\cos \alpha_0\,{\bf v} + \cos L\,\sin \alpha_0\,{\bf u} + \sin L\,{\bf p}.$$ (23)

Similarly, from Eqs. (6) and (7),

$${\bf e} = -\sin \alpha_0\,{\bf v} + \cos\epsilon\,\cos \alpha_0\,{\bf s} - \sin\epsilon\,\cos \alpha_0\,{\bf q},$$ (24)

$${\bf n} = -\sin L\,\cos \alpha_0\,{\bf v} + (\cos L\,\sin \epsilon-\sin L\,\cos \epsilon\,\sin \alpha_0)\,{\bf s} + (\cos L\,\cos \epsilon$$

$$+\sin L\,\sin \epsilon\,\sin \alpha_0)\,{\bf q},$$ (25)

$${\bf z} = \cos L\,\cos \alpha_0\,{\bf v} + (\sin L\,\sin\epsilon + \cos L\,\cos\epsilon\,\sin \alpha_0)\,{\bf s} + (\sin L\,\cos\epsilon$$

$$-\cos L\,\sin\epsilon\,\sin \alpha_0)\,{\bf q}.$$ (26)