


Next: Ecliptic Coordinates
Up: Spherical Astronomy
Previous: Celestial Coordinates
During the course of a year, the sun's intrinsic motion causes it to trace out a fixed circle which bisects the celestial sphere. This circle is known as the ecliptic. The sun travels around the ecliptic from west to east (i.e., in the opposite direction
to the celestial sphere's diurnal rotation). Moreover, the ecliptic circle is inclined at a fixed angle of
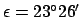 to the celestial equator.
This angle actually represents the fixed inclination of the earth's axis of rotation to the normal to its orbital
plane.
to the celestial equator.
This angle actually represents the fixed inclination of the earth's axis of rotation to the normal to its orbital
plane.![[*]](footnote.png)
Figure 5:
The ecliptic circle. 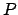 ,
, 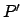 ,
,  ,
, 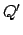 ,
, 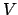 ,
, 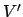 ,
, 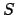 ,
and
,
and 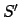 denote the north celestial pole, south celestial pole, north ecliptic pole, south
ecliptic pole, vernal equinox, autumnal equinox, summer solstice, and winter
solstice, respectively.
denote the north celestial pole, south celestial pole, north ecliptic pole, south
ecliptic pole, vernal equinox, autumnal equinox, summer solstice, and winter
solstice, respectively. 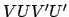 is the celestial equator,
is the celestial equator, 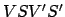 the ecliptic, and
the ecliptic, and  the
celestial axis.
the
celestial axis.
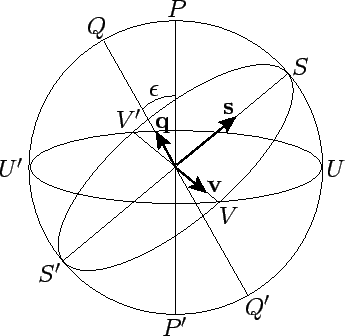 |
The vernal equinox, 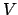 , is defined as the point at which the ecliptic crosses the celestial equator
from south to north (in the direction of the sun's ecliptic motion)--see Fig. 5. Likewise, the autumnal equinox,
, is defined as the point at which the ecliptic crosses the celestial equator
from south to north (in the direction of the sun's ecliptic motion)--see Fig. 5. Likewise, the autumnal equinox, 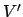 , is the point at which the ecliptic crosses the
celestial equator from north to south. In addition, the summer solstice,
, is the point at which the ecliptic crosses the
celestial equator from north to south. In addition, the summer solstice, 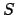 , is the
point on the ecliptic which is furthest north of the celestial equator, whereas the
winter solstice,
, is the
point on the ecliptic which is furthest north of the celestial equator, whereas the
winter solstice, 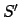 , is the point which is furthest south. It follows that the lines
, is the point which is furthest south. It follows that the lines  and
and 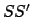 are perpendicular. Let
are perpendicular. Let 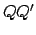 be the normal to the plane of the ecliptic which passes through the earth, as shown in Fig. 5.
Here,
be the normal to the plane of the ecliptic which passes through the earth, as shown in Fig. 5.
Here,  is termed the northern ecliptic pole, and
is termed the northern ecliptic pole, and 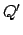 the southern ecliptic pole.
It is easily demonstrated that
the southern ecliptic pole.
It is easily demonstrated that
where  is a unit vector which is directed from the earth to the summer solstice, and
is a unit vector which is directed from the earth to the summer solstice, and 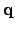 a unit vector which is directed from the earth to the north ecliptic pole--see Fig. 5. We can also write
a unit vector which is directed from the earth to the north ecliptic pole--see Fig. 5. We can also write
Thus, 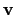 ,
,  , and
, and 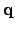 constitute another right-handed, mutually perpendicular, set of unit vectors.
constitute another right-handed, mutually perpendicular, set of unit vectors.
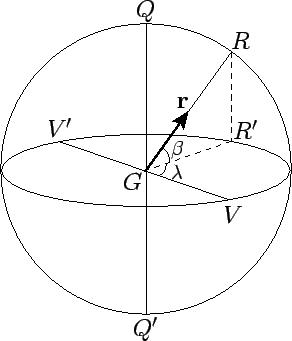
Figure 6:
Ecliptic coordinates. 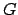 is the earth,
is the earth, 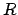 a celestial
object, and
a celestial
object, and  its projection onto the ecliptic plane,
its projection onto the ecliptic plane, 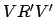 .
.
 |



Next: Ecliptic Coordinates
Up: Spherical Astronomy
Previous: Celestial Coordinates
Richard Fitzpatrick
2010-07-21

![[*]](footnote.png)

![]() , is defined as the point at which the ecliptic crosses the celestial equator
from south to north (in the direction of the sun's ecliptic motion)--see Fig. 5. Likewise, the autumnal equinox,
, is defined as the point at which the ecliptic crosses the celestial equator
from south to north (in the direction of the sun's ecliptic motion)--see Fig. 5. Likewise, the autumnal equinox, ![]() , is the point at which the ecliptic crosses the
celestial equator from north to south. In addition, the summer solstice,
, is the point at which the ecliptic crosses the
celestial equator from north to south. In addition, the summer solstice, ![]() , is the
point on the ecliptic which is furthest north of the celestial equator, whereas the
winter solstice,
, is the
point on the ecliptic which is furthest north of the celestial equator, whereas the
winter solstice, ![]() , is the point which is furthest south. It follows that the lines
, is the point which is furthest south. It follows that the lines ![]() and
and ![]() are perpendicular. Let
are perpendicular. Let ![]() be the normal to the plane of the ecliptic which passes through the earth, as shown in Fig. 5.
Here,
be the normal to the plane of the ecliptic which passes through the earth, as shown in Fig. 5.
Here, ![]() is termed the northern ecliptic pole, and
is termed the northern ecliptic pole, and ![]() the southern ecliptic pole.
It is easily demonstrated that
the southern ecliptic pole.
It is easily demonstrated that
