

Next: Signs of the Zodiac
Up: Spherical Astronomy
Previous: Ecliptic Circle
It is convenient to specify the positions of the sun, moon, and planets in the sky using
a pair of angular coordinates, 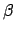 and
and 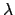 , which are measured with respect to the
ecliptic, rather than the celestial equator. Let
, which are measured with respect to the
ecliptic, rather than the celestial equator. Let 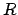 denote a celestial object, and
denote a celestial object, and 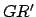 the
projection of the line
the
projection of the line 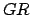 onto the plane of the ecliptic,
onto the plane of the ecliptic, 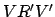 --see Fig. 6. The coordinate
--see Fig. 6. The coordinate 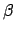 , which
is known as ecliptic latitude, is the angle subtended between
, which
is known as ecliptic latitude, is the angle subtended between 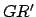 and
and 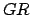 . Objects north
of the ecliptic plane have positive ecliptic latitudes, and vice versa. The coordinate
. Objects north
of the ecliptic plane have positive ecliptic latitudes, and vice versa. The coordinate 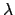 ,
which is known as ecliptic longitude, is the angle subtended between
,
which is known as ecliptic longitude, is the angle subtended between 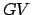 and
and
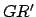 . Ecliptic longitude increases from west to east (i.e., in the same direction that the sun travels
around the ecliptic). (Again, in this treatise,
. Ecliptic longitude increases from west to east (i.e., in the same direction that the sun travels
around the ecliptic). (Again, in this treatise, 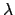 is measured relative
to the mean equinox at date, unless specified otherwise.)
Note that the basis vectors in the ecliptic coordinate system are
is measured relative
to the mean equinox at date, unless specified otherwise.)
Note that the basis vectors in the ecliptic coordinate system are
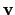 ,
, 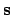 , and
, and 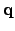 , whereas the corresponding basis vectors in the
celestial coordinate system are
, whereas the corresponding basis vectors in the
celestial coordinate system are
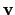 ,
, 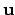 , and
, and 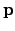 --see Figs. 3 and 5. By analogy with Eqs. (1)-(3), we can write
--see Figs. 3 and 5. By analogy with Eqs. (1)-(3), we can write
where 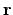 is a unit vector which is directed from
is a unit vector which is directed from 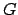 to
to 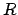 .
Hence, it follows from Eqs. (1), (4), and (5) that
.
Hence, it follows from Eqs. (1), (4), and (5) that
These expressions specify the transformation from celestial to ecliptic
coordinates. The inverse transformation follows from Eqs. (2), (3), and (6)-(8):
Figures 15 and 16 show all stars of visible magnitude less than 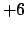 lying
within
lying
within 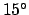 of the ecliptic. Table 1 gives the ecliptic longitudes, ecliptic latitudes, and
visible magnitudes of a selection
of these stars which lie within
of the ecliptic. Table 1 gives the ecliptic longitudes, ecliptic latitudes, and
visible magnitudes of a selection
of these stars which lie within 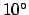 of the ecliptic. The figures and table can
be used
to convert ecliptic longitude and latitude into approximate position
in the sky against the backdrop of the fixed stars.
of the ecliptic. The figures and table can
be used
to convert ecliptic longitude and latitude into approximate position
in the sky against the backdrop of the fixed stars.


Next: Signs of the Zodiac
Up: Spherical Astronomy
Previous: Ecliptic Circle
Richard Fitzpatrick
2010-07-21
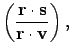
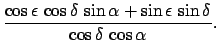
![]() lying
within
lying
within ![]() of the ecliptic. Table 1 gives the ecliptic longitudes, ecliptic latitudes, and
visible magnitudes of a selection
of these stars which lie within
of the ecliptic. Table 1 gives the ecliptic longitudes, ecliptic latitudes, and
visible magnitudes of a selection
of these stars which lie within ![]() of the ecliptic. The figures and table can
be used
to convert ecliptic longitude and latitude into approximate position
in the sky against the backdrop of the fixed stars.
of the ecliptic. The figures and table can
be used
to convert ecliptic longitude and latitude into approximate position
in the sky against the backdrop of the fixed stars.