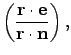Next: Meridian Transits
Up: Spherical Astronomy
Previous: Local Horizon and Meridian
It is convenient to specify the positions of celestial objects in the sky, when viewed from
a particular observation site,  , on the earth's surface, using a pair of angular coordinates,
, on the earth's surface, using a pair of angular coordinates,  and
and  ,
which are measured with respect to the local horizon. Let
,
which are measured with respect to the local horizon. Let 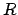 denote
a celestial object, and
denote
a celestial object, and 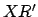 the projection of the line
the projection of the line 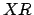 onto the
horizontal plane,
onto the
horizontal plane, 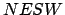 --see Fig. 11. The coordinate
--see Fig. 11. The coordinate 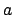 , which
is known as altitude, is the angle subtended between
, which
is known as altitude, is the angle subtended between 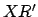 and
and
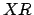 . Objects above the horizon have positive altitudes, whereas
objects below the horizon have negative altitudes. The
zenith has altitude
. Objects above the horizon have positive altitudes, whereas
objects below the horizon have negative altitudes. The
zenith has altitude 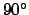 , and the horizon altitude
, and the horizon altitude 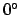 . The coordinate
. The coordinate 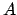 ,
which is known as azimuth, is the angle subtended between
,
which is known as azimuth, is the angle subtended between
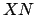 and
and 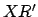 . Azimuth increases from the north towards the east. Thus, the
north, east, south, and west compass points have azimuths of
. Azimuth increases from the north towards the east. Thus, the
north, east, south, and west compass points have azimuths of
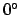 ,
, 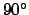 ,
, 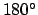 , and
, and 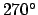 , respectively.
Note that the basis vectors in the horizontal coordinate system are
, respectively.
Note that the basis vectors in the horizontal coordinate system are 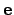 ,
,
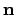 , and
, and 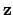 , whereas the corresponding basis vectors in the
celestial coordinate system are
, whereas the corresponding basis vectors in the
celestial coordinate system are 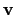 ,
, 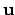 , and
, and 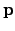 --see Figs. 3 and 8. By analogy with Eqs. (1)--(3), we can write
--see Figs. 3 and 8. By analogy with Eqs. (1)--(3), we can write
where 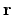 is a unit vector directed from
is a unit vector directed from 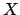 to
to 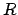 .
Hence, it follows from Eqs. (1), and (22)-(23), that
.
Hence, it follows from Eqs. (1), and (22)-(23), that
These expressions allow us to calculate the altitude and azimuth of a
celestial object of declination 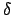 and right ascension
and right ascension 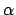 which is viewed from an observation site on the earth's surface of terrestrial latitude
which is viewed from an observation site on the earth's surface of terrestrial latitude 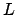 at an instant in time
when celestial objects of right ascension
at an instant in time
when celestial objects of right ascension 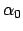 are culminating at the meridian.
According to Eqs. (8), and (25)-(26),
the altitude and azimuth of a similarly viewed point on the ecliptic (i.e.,
are culminating at the meridian.
According to Eqs. (8), and (25)-(26),
the altitude and azimuth of a similarly viewed point on the ecliptic (i.e., 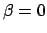 ) of ecliptic
longitude
) of ecliptic
longitude 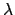 are given by
are given by
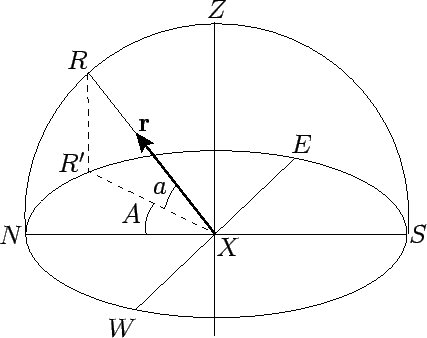
Figure 11:
Horizontal coordinates.  is a celestial object, and
is a celestial object, and
 its projection onto the horizontal plane,
its projection onto the horizontal plane,  .
.
 |



Next: Meridian Transits
Up: Spherical Astronomy
Previous: Local Horizon and Meridian
Richard Fitzpatrick
2010-07-21