

Next: Determination of Conjunction and
Up: The Inferior Planets
Previous: Determination of Ecliptic Longitude
The ecliptic longitude of Venus can be determined with the aid of Tables 58-60. Table 58 allows
the mean longitude, 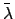 , and the mean anomaly,
, and the mean anomaly, 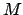 , of Venus to be calculated as functions of
time. Next, Table 59 permits the equation of center,
, of Venus to be calculated as functions of
time. Next, Table 59 permits the equation of center, 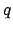 , and the radial anomaly,
, and the radial anomaly, 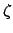 , to
be determined as functions of the mean anomaly. Finally, Table 60 allows the quantities
, to
be determined as functions of the mean anomaly. Finally, Table 60 allows the quantities
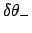 ,
, 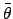 , and
, and
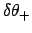 to be calculated as functions of the epicyclic
anomaly,
to be calculated as functions of the epicyclic
anomaly, 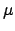 .
.
The procedure for using the tables is as follows:
- Determine the fractional Julian day number,
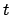 , corresponding to the date and time
at which the ecliptic longitude is to be calculated with the aid of Tables 27-29. Form
, corresponding to the date and time
at which the ecliptic longitude is to be calculated with the aid of Tables 27-29. Form
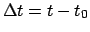 , where
, where
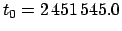 is the epoch.
is the epoch.
- Calculate the ecliptic longitude,
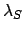 , and radial anomaly,
, and radial anomaly,
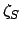 , of the sun using the procedure set out in Sect. 5.1.
, of the sun using the procedure set out in Sect. 5.1.
- Enter Table 58 with the digit for each power of 10
in
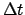 and take out the corresponding values of
and take out the corresponding values of
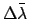 and
and 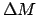 . If
. If 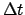 is negative then the corresponding
values are also negative.
The value of the mean longitude,
is negative then the corresponding
values are also negative.
The value of the mean longitude, 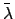 , is the
sum of all the
, is the
sum of all the
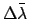 values plus value of
values plus value of 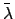 at the epoch. Likewise, the value of the mean anomaly,
at the epoch. Likewise, the value of the mean anomaly, 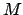 , is
the sum of all the
, is
the sum of all the 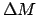 values plus the value of
values plus the value of 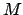 at the epoch.
Add as many multiples of
at the epoch.
Add as many multiples of 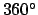 to
to 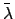 and
and 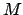 as is required to make them both fall in the range
as is required to make them both fall in the range 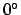 to
to 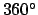 . Round
. Round 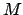 to the nearest degree.
to the nearest degree.
- Enter Table 59 with the value of
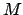 and take out the
corresponding value of the equation of center,
and take out the
corresponding value of the equation of center, 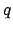 , and the radial anomaly,
, and the radial anomaly, 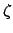 . It is necessary to interpolate if
. It is necessary to interpolate if 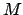 is odd.
is odd.
- Form the epicyclic anomaly,
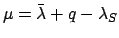 . Add as many multiples of
. Add as many multiples of 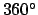 to
to 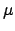 as is required to make it fall in the range
as is required to make it fall in the range 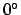 to
to 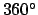 . Round
. Round 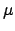 to the nearest degree.
to the nearest degree.
- Enter Table 60 with the value of
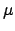 and take
out the corresponding values of
and take
out the corresponding values of
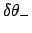 ,
, 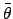 , and
, and
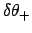 . If
. If
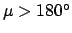 then it is necessary to make use
of the identities
then it is necessary to make use
of the identities
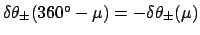 and
and
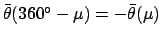 .
.
- Form
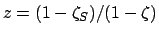 .
.
- Obtain the values of
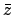 and
and 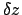 from Table 5.
Form
from Table 5.
Form
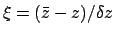 .
.
- Enter Table 17 with the value of
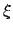 and take out
the corresponding values of
and take out
the corresponding values of 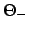 and
and 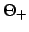 . If
. If 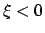 then
it is necessary to use the identities
then
it is necessary to use the identities
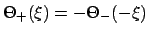 and
and
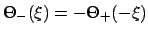 .
.
- Form the equation of the epicycle,
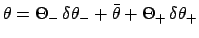 .
.
- The ecliptic longitude,
 , is the sum of the ecliptic longitude of the sun,
, is the sum of the ecliptic longitude of the sun,  , and the equation
of the epicycle,
, and the equation
of the epicycle, 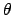 . If necessary convert
. If necessary convert 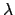 into an angle in the range
into an angle in the range 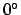 to
to 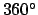 . The decimal fraction can
be converted into arc minutes
using Table 31. Round to the nearest arc minute. The final result
can be written in terms of the signs of the zodiac using the table in Sect. 2.6.
. The decimal fraction can
be converted into arc minutes
using Table 31. Round to the nearest arc minute. The final result
can be written in terms of the signs of the zodiac using the table in Sect. 2.6.
Two examples of this procedure are given below.
Example 1: May 5, 2005 CE, 00:00 UT:
From Cha. 8,
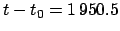 JD,
JD,
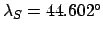 , and
, and
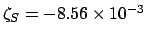 . Making use of
Table 58, we find:
. Making use of
Table 58, we find:
| |
|
|
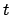 (JD) (JD) |
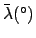 |
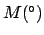 |
| |
|
|
| +1000 |
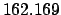 |
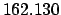 |
| +900 |
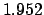 |
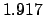 |
| +50 |
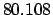 |
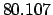 |
| +.5 |
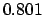 |
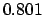 |
| Epoch |
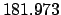 |
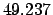 |
| |
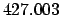 |
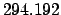 |
| Modulus |
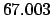 |
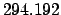 |
| |
|
|
Given that
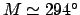 , Table 59 yields
, Table 59 yields
so
It follows from Table 60
that
Now,
However, from Table 5,
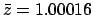 and
and
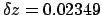 , so
, so
According to Table 17,
so
Finally,
Thus,
the ecliptic longitude of Venus at 00:00 UT on May 5, 2005 CE was 23TA45.
Example 2: December 25, 1800 CE, 00:00 UT:
From Cha. 8,
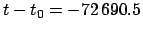 JD,
JD,
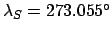 , and
, and
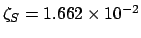 . Making use of
Table 58, we find:
. Making use of
Table 58, we find:
| |
|
|
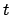 (JD) (JD) |
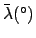 |
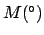 |
| |
|
|
| -70,000 |
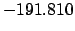 |
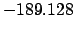 |
| -2,000 |
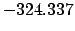 |
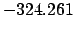 |
| -600 |
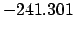 |
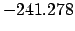 |
| -90 |
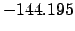 |
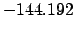 |
| -.5 |
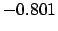 |
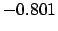 |
| Epoch |
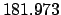 |
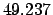 |
| |
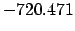 |
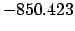 |
| Modulus |
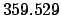 |
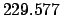 |
| |
|
|
Given that
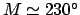 , Table 59 yields
, Table 59 yields
so
It follows from Table 60
that
Now,
so
According to Table 17,
so
Finally,
Thus,
the ecliptic longitude of Venus at 00:00 UT on December 25, 1800 CE was 8AQ5.


Next: Determination of Conjunction and
Up: The Inferior Planets
Previous: Determination of Ecliptic Longitude
Richard Fitzpatrick
2010-07-21
![]() JD,
JD,
![]() , and
, and
![]() . Making use of
Table 58, we find:
. Making use of
Table 58, we find:
![]() JD,
JD,
![]() , and
, and
![]() . Making use of
Table 58, we find:
. Making use of
Table 58, we find: