

Next: Example Longitude Calculations
Up: The Sun
Previous: The Sun
Determination of Ecliptic Longitude
Our solar longitude model is sketched in Figure 21. From a geocentric point of view, the sun,  , appears to execute
a (counterclockwise) Keplerian orbit of major radius
, appears to execute
a (counterclockwise) Keplerian orbit of major radius 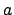 , and eccentricity
, and eccentricity  , about the
earth,
, about the
earth,  . As has already been mentioned, the circle traced out by the sun on the celestial sphere is
known as the ecliptic circle. This circle is inclined at
. As has already been mentioned, the circle traced out by the sun on the celestial sphere is
known as the ecliptic circle. This circle is inclined at 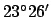 to
the celestial equator, which is the projection of the earth's equator onto
the celestial sphere.
Suppose that the angle subtended at the earth between the vernal equinox (i.e., the point at which the ecliptic crosses the celestial equator from
south to north) and the
sun's perigee (i.e., the point of closest approach to the earth) is
to
the celestial equator, which is the projection of the earth's equator onto
the celestial sphere.
Suppose that the angle subtended at the earth between the vernal equinox (i.e., the point at which the ecliptic crosses the celestial equator from
south to north) and the
sun's perigee (i.e., the point of closest approach to the earth) is
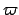 . This
angle is termed the longitude of the perigee, and
is assumed
to vary linearly with time: i.e.,
. This
angle is termed the longitude of the perigee, and
is assumed
to vary linearly with time: i.e.,
 |
(95) |
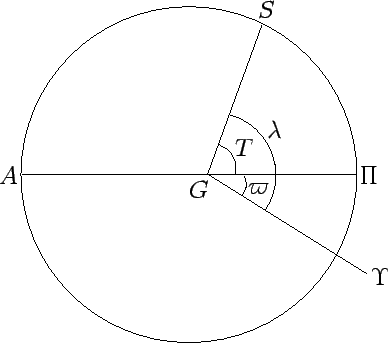
Figure 21:
The apparent orbit of the sun about the earth. Here,  ,
,  ,
, 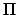 ,
, 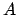 ,
, 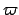 ,
,  ,
, 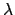 , and
, and 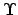 represent the sun, earth, perigee, apogee, longitude of the perigee, true anomaly, ecliptic longitude, and
vernal equinox, respectively. View is from northern ecliptic pole. The sun orbits counterclockwise.
represent the sun, earth, perigee, apogee, longitude of the perigee, true anomaly, ecliptic longitude, and
vernal equinox, respectively. View is from northern ecliptic pole. The sun orbits counterclockwise.
 |
The sun's ecliptic
longitude is defined as the angle subtended at the earth between the vernal equinox and the sun.
Hence, from Fig. 21,
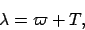 |
(96) |
where  is the true anomaly (see Cha. 4). By analogy, the mean longitude is written
is the true anomaly (see Cha. 4). By analogy, the mean longitude is written
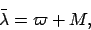 |
(97) |
where 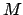 is the mean anomaly (see Cha. 4). It follows from Eq. (82) that
is the mean anomaly (see Cha. 4). It follows from Eq. (82) that
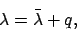 |
(98) |
where
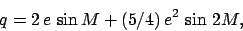 |
(99) |
is called the equation of center. Note that 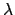 ,
, 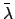 ,
,  , and
, and 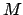 are usually written as angles in the range
are usually written as angles in the range
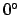 to
to 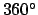 , whereas
, whereas 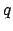 is generally written as an
angle in the range
is generally written as an
angle in the range 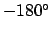 to
to  .
.
The mean longitude increases
uniformly with time (since both 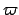 and
and 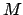 increase uniformly with time) as
increase uniformly with time) as
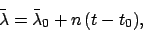 |
(100) |
where
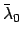 is termed the
mean longitude at epoch,
is termed the
mean longitude at epoch,
 the rate of motion in mean longitude, and
the rate of motion in mean longitude, and  the epoch.
We can also write
the epoch.
We can also write
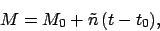 |
(101) |
where
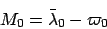 |
(102) |
is called the mean anomaly at epoch, and
 |
(103) |
the rate of motion in mean anomaly.
Our procedure for determining the ecliptic longitude of the sun is described
below.
The requisite orbital elements (i.e.,  ,
,  ,
,  ,
,
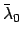 , and
, and 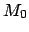 ) for the J2000 epoch (i.e., 12:00 UT on January 1, 2000 CE, which corresponds to
) for the J2000 epoch (i.e., 12:00 UT on January 1, 2000 CE, which corresponds to
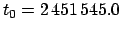 JD) are listed
in Table 30. These elements are calculated
on the assumption that the vernal equinox precesses at the uniform
rate of
JD) are listed
in Table 30. These elements are calculated
on the assumption that the vernal equinox precesses at the uniform
rate of
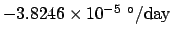 .
The ecliptic longitude of the sun is specified by the
following formulae:
.
The ecliptic longitude of the sun is specified by the
following formulae:
These formulae are capable of matching NASA ephemeris data
during the years 1995-2006 CE (see http://ssd.jpl.nasa.gov/) with a mean error of 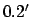 and a maximum error of
and a maximum error of 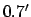 .
.
The ecliptic longitude of the sun can be calculated with the aid of Tables 32 and 33.
Table 32 allows the mean longitude, 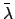 , and mean anomaly,
, and mean anomaly,
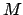 , of the
sun to be determined as functions of time. Table 33 specifies the equation of center,
, of the
sun to be determined as functions of time. Table 33 specifies the equation of center, 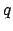 , as a
function of the mean anomaly.
, as a
function of the mean anomaly.
The procedure for using the tables is as follows:
- Determine the fractional Julian day number,
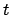 , corresponding to the date and time
at which the sun's ecliptic longitude is to be calculated with the aid of Tables 27-29. Form
, corresponding to the date and time
at which the sun's ecliptic longitude is to be calculated with the aid of Tables 27-29. Form
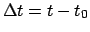 , where
, where
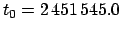 is the epoch.
is the epoch.
- Enter Table 32 with the digit for each power of 10
in
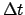 and take out the corresponding values of
and take out the corresponding values of
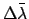 and
and 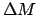 . If
. If 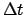 is negative then the corresponding
values are also negative.
The value of the mean longitude,
is negative then the corresponding
values are also negative.
The value of the mean longitude, 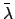 , is the
sum of all the
, is the
sum of all the
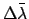 values plus the value of
values plus the value of 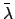 at the epoch. Likewise, the value of the mean anomaly,
at the epoch. Likewise, the value of the mean anomaly, 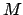 , is
the sum of all the
, is
the sum of all the 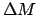 values plus the value of
values plus the value of 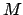 at the epoch.
Add as many multiples of
at the epoch.
Add as many multiples of 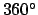 to
to 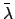 and
and 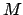 as is required to make them both fall in the range
as is required to make them both fall in the range 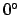 to
to 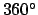 . Round
. Round 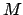 to the nearest degree.
to the nearest degree.
- Enter Table 33 with the value of
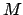 and take out the
corresponding value of the equation of center,
and take out the
corresponding value of the equation of center, 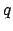 , and the radial anomaly,
, and the radial anomaly, 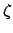 . (The latter step is only necessary if the ecliptic longitude of the sun is
to be used to determine that of a planet.) It is necessary to interpolate if
. (The latter step is only necessary if the ecliptic longitude of the sun is
to be used to determine that of a planet.) It is necessary to interpolate if 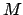 is odd.
is odd.
- The ecliptic longitude,
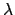 , is the sum of the mean longitude,
, is the sum of the mean longitude, 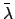 , and the equation of center,
, and the equation of center, 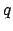 . If necessary, convert
. If necessary, convert 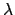 into an angle in the range
into an angle in the range 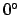 to
to 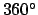 .
The decimal fraction can be converted into arc minutes
using Table 31. Round to the nearest arc minute.
.
The decimal fraction can be converted into arc minutes
using Table 31. Round to the nearest arc minute.
Two examples of the use of this procedure are given below.


Next: Example Longitude Calculations
Up: The Sun
Previous: The Sun
Richard Fitzpatrick
2010-07-21

![]() and
and ![]() increase uniformly with time) as
increase uniformly with time) as
![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and ![]() ) for the J2000 epoch (i.e., 12:00 UT on January 1, 2000 CE, which corresponds to
) for the J2000 epoch (i.e., 12:00 UT on January 1, 2000 CE, which corresponds to
![]() JD) are listed
in Table 30. These elements are calculated
on the assumption that the vernal equinox precesses at the uniform
rate of
JD) are listed
in Table 30. These elements are calculated
on the assumption that the vernal equinox precesses at the uniform
rate of
![]() .
The ecliptic longitude of the sun is specified by the
following formulae:
.
The ecliptic longitude of the sun is specified by the
following formulae:
![]() , and mean anomaly,
, and mean anomaly,
![]() , of the
sun to be determined as functions of time. Table 33 specifies the equation of center,
, of the
sun to be determined as functions of time. Table 33 specifies the equation of center, ![]() , as a
function of the mean anomaly.
, as a
function of the mean anomaly.