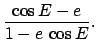

Next: Model of Hipparchus
Up: Geometric Planetary Orbit Models
Previous: Introduction
Kepler's geometric model of a heliocentric planetary orbit is summed up in his three well-known laws of planetary motion.
According to Kepler's first law, all planetary orbits are ellipses which are confocal with the sun and lie in a
fixed plane.
Moreover, according to Kepler's second law, the radius vector which connects the sun to a given planet sweeps out equal areas in equal time intervals.
Figure 17:
A Keplerian orbit.
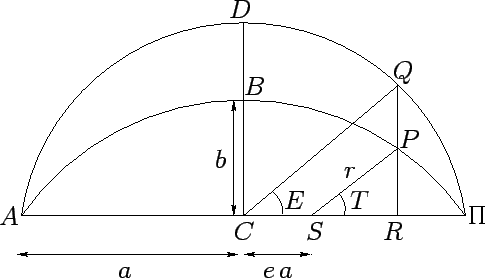 |
Consider Figure 17.  is half of an elliptical planetary orbit. Furthermore,
is half of an elliptical planetary orbit. Furthermore, 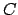 is the
geometric center of the orbit,
is the
geometric center of the orbit, 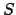 the focus at which the sun is located,
the focus at which the sun is located,
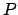 the instantaneous position of the planet,
the instantaneous position of the planet, 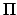 the perihelion point (i.e., the planet's point of closest approach to the sun),
and
the perihelion point (i.e., the planet's point of closest approach to the sun),
and 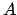 the aphelion point (i.e., the point of furthest distance from the sun). The ellipse is symmetric about
the aphelion point (i.e., the point of furthest distance from the sun). The ellipse is symmetric about
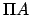 , which is termed the major axis, and about
, which is termed the major axis, and about 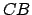 ,
which is termed the minor axis.
The length
,
which is termed the minor axis.
The length 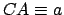 is called the orbital
major radius. The length
is called the orbital
major radius. The length 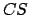 represents the displacement of the sun from
the geometric center of the orbit, and is generally written
represents the displacement of the sun from
the geometric center of the orbit, and is generally written 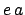 , where
, where 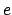 is termed the
orbital eccentricity, where
is termed the
orbital eccentricity, where 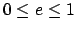 . The length
. The length
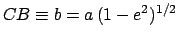 is called
the orbital minor radius.
The length
is called
the orbital minor radius.
The length 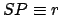 represents the radial distance of the planet from the sun.
Finally, the angle
represents the radial distance of the planet from the sun.
Finally, the angle 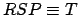 is the angular bearing of the planet from the sun,
relative to the major axis of the orbit, and is termed the true anomaly.
is the angular bearing of the planet from the sun,
relative to the major axis of the orbit, and is termed the true anomaly.
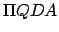 is half of a circle whose geometric center is
is half of a circle whose geometric center is 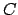 , and whose
radius is
, and whose
radius is 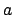 . Hence, the circle passes through the perihelion and aphelion
points.
. Hence, the circle passes through the perihelion and aphelion
points. 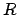 is the point at which the perpendicular from
is the point at which the perpendicular from 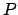 meets the major axis
meets the major axis 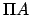 . The point where
. The point where 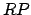 produced
meets circle
produced
meets circle 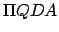 is denoted
is denoted 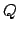 . Finally,
the angle
. Finally,
the angle 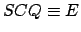 is called the elliptic anomaly.
is called the elliptic anomaly.
Now, the equation of the ellipse 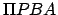 is
is
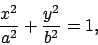 |
(60) |
where 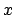 and
and 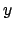 are the perpendicular distances from the minor and major
axes, respectively. Likewise, the equation of the circle
are the perpendicular distances from the minor and major
axes, respectively. Likewise, the equation of the circle 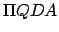 is
is
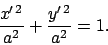 |
(61) |
Hence, if 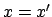 then
then
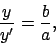 |
(62) |
and it follows that
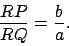 |
(63) |
Now, 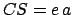 . Furthermore, it is easily demonstrated that
. Furthermore, it is easily demonstrated that
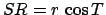 ,
, 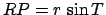 ,
, 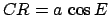 , and
, and 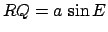 . Consequently, Eq. (63) yields
. Consequently, Eq. (63) yields
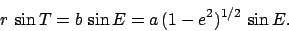 |
(64) |
Also, since 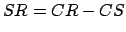 , we have
, we have
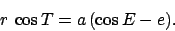 |
(65) |
Taking the square root of the sum of the squares of the previous two equations, we obtain
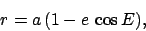 |
(66) |
which can be combined with Eq. (65) to give
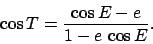 |
(67) |
Now, according to Kepler's second law,
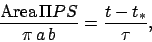 |
(68) |
where 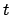 is the time at which the planet passes point
is the time at which the planet passes point 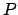 ,
, 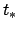 the time at which it passes the perihelion point,
and
the time at which it passes the perihelion point,
and 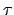 the orbital period.
However,
the orbital period.
However,
But,
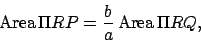 |
(70) |
since 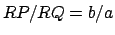 for all values of
for all values of 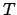 . In addition,
. In addition,
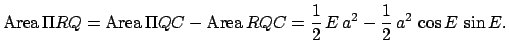 |
|
|
(71) |
Hence, we can write
 |
(72) |
According to Eqs. (64) and (65),
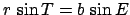 , and
, and
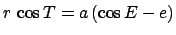 , so
the above expression reduces to
, so
the above expression reduces to
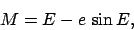 |
(73) |
where
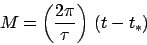 |
(74) |
is an angle which is zero at the perihelion point, increases uniformly in time, and has a repetition period which
matches the period of the planetary orbit. This angle is termed the mean anomaly.
In summary, the radial and angular polar coordinates, 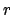 and
and 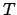 , respectively,
of a planet in a Keplerian orbit about the sun are specified as implicit functions
of the mean anomaly, which is a linear function of time, by the
following three equations:
, respectively,
of a planet in a Keplerian orbit about the sun are specified as implicit functions
of the mean anomaly, which is a linear function of time, by the
following three equations:
It turns out that the earth and the five visible planets all possess low eccentricity orbits characterized by 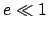 . Hence, it is a good approximation to expand the above three equations
using
. Hence, it is a good approximation to expand the above three equations
using 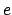 as a small parameter. To second-order, we
get
as a small parameter. To second-order, we
get
Finally, these equations can be combined to give 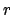 and
and 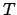 as explicit functions of the
mean anomaly:
as explicit functions of the
mean anomaly:


Next: Model of Hipparchus
Up: Geometric Planetary Orbit Models
Previous: Introduction
Richard Fitzpatrick
2010-07-21

![]() is half of an elliptical planetary orbit. Furthermore,
is half of an elliptical planetary orbit. Furthermore, ![]() is the
geometric center of the orbit,
is the
geometric center of the orbit, ![]() the focus at which the sun is located,
the focus at which the sun is located,
![]() the instantaneous position of the planet,
the instantaneous position of the planet, ![]() the perihelion point (i.e., the planet's point of closest approach to the sun),
and
the perihelion point (i.e., the planet's point of closest approach to the sun),
and ![]() the aphelion point (i.e., the point of furthest distance from the sun). The ellipse is symmetric about
the aphelion point (i.e., the point of furthest distance from the sun). The ellipse is symmetric about
![]() , which is termed the major axis, and about
, which is termed the major axis, and about ![]() ,
which is termed the minor axis.
The length
,
which is termed the minor axis.
The length ![]() is called the orbital
major radius. The length
is called the orbital
major radius. The length ![]() represents the displacement of the sun from
the geometric center of the orbit, and is generally written
represents the displacement of the sun from
the geometric center of the orbit, and is generally written ![]() , where
, where ![]() is termed the
orbital eccentricity, where
is termed the
orbital eccentricity, where ![]() . The length
. The length
![]() is called
the orbital minor radius.
The length
is called
the orbital minor radius.
The length ![]() represents the radial distance of the planet from the sun.
Finally, the angle
represents the radial distance of the planet from the sun.
Finally, the angle ![]() is the angular bearing of the planet from the sun,
relative to the major axis of the orbit, and is termed the true anomaly.
is the angular bearing of the planet from the sun,
relative to the major axis of the orbit, and is termed the true anomaly.
![]() is half of a circle whose geometric center is
is half of a circle whose geometric center is ![]() , and whose
radius is
, and whose
radius is ![]() . Hence, the circle passes through the perihelion and aphelion
points.
. Hence, the circle passes through the perihelion and aphelion
points. ![]() is the point at which the perpendicular from
is the point at which the perpendicular from ![]() meets the major axis
meets the major axis ![]() . The point where
. The point where ![]() produced
meets circle
produced
meets circle ![]() is denoted
is denoted ![]() . Finally,
the angle
. Finally,
the angle ![]() is called the elliptic anomaly.
is called the elliptic anomaly.
![]() is
is
![]() . Furthermore, it is easily demonstrated that
. Furthermore, it is easily demonstrated that
![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Consequently, Eq. (63) yields
. Consequently, Eq. (63) yields
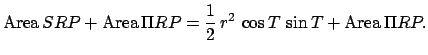
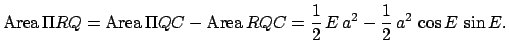
![]() and
and ![]() , respectively,
of a planet in a Keplerian orbit about the sun are specified as implicit functions
of the mean anomaly, which is a linear function of time, by the
following three equations:
, respectively,
of a planet in a Keplerian orbit about the sun are specified as implicit functions
of the mean anomaly, which is a linear function of time, by the
following three equations: