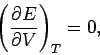Next: Heat capacity or specific
Up: Classical thermodynamics
Previous: Introduction
Let us start our discussion by considering the simplest possible macroscopic
system: i.e., an ideal gas. All of the thermodynamic properties of an ideal gas
are summed up in its equation of state, which determines the relationship
between its pressure, volume, and temperature. Unfortunately, classical thermodynamics is unable to tell us what this equation of state is from first principles.
In fact, classical thermodynamics cannot tell us anything from
first principles. We always have to provide some information to begin
with before classical thermodynamics can
generate any new results.
This initial information may come from statistical physics (i.e., from our
knowledge of the microscopic structure of the system under
consideration), but, more usually, it is
entirely empirical in nature
(i.e., it is the result of experiments). Of course, the ideal gas
law was first discovered empirically by Robert Boyle, but, nowadays,
we can justify it from statistical arguments. Recall
(from Sect. 3.8), that the number of accessible states of
a monotonic ideal gas varies like
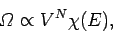 |
(265) |
where  is the number of atoms, and
is the number of atoms, and 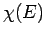 depends only on the energy
of the gas (and is
independent of the volume). We obtained this result by integrating over the
volume of accessible phase-space. Since the energy of an ideal gas is independent of
the
particle coordinates (because there are no interatomic forces), the integrals over the
coordinates just reduced to
depends only on the energy
of the gas (and is
independent of the volume). We obtained this result by integrating over the
volume of accessible phase-space. Since the energy of an ideal gas is independent of
the
particle coordinates (because there are no interatomic forces), the integrals over the
coordinates just reduced to  simultaneous volume integrals, giving the
simultaneous volume integrals, giving the
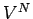 factor
in the above expression. The integrals over the particle momenta were more
complicated, but were clearly completely independent of
factor
in the above expression. The integrals over the particle momenta were more
complicated, but were clearly completely independent of 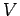 ,
giving the
,
giving the 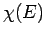 factor in the above expression.
Now, we have a statistical rule which tells us that
factor in the above expression.
Now, we have a statistical rule which tells us that
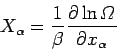 |
(266) |
[see Eq. (197)],
where 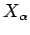 is the mean force conjugate to the external parameter
is the mean force conjugate to the external parameter 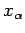 (i.e.,
(i.e.,
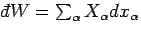 ), and
), and
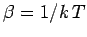 .
For
an ideal gas, the only external parameter is the volume, and its conjugate
force is the pressure (since
.
For
an ideal gas, the only external parameter is the volume, and its conjugate
force is the pressure (since
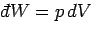 ). So, we can write
). So, we can write
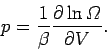 |
(267) |
If we simply apply this rule to Eq. (265), we obtain
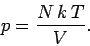 |
(268) |
However, 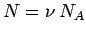 , where
, where 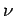 is the number of moles, and
is the number of moles, and 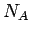 is Avagadro's
number. Also,
is Avagadro's
number. Also, 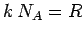 , where
, where  is the ideal gas constant. This allows us to
write the equation of state in its usual form
is the ideal gas constant. This allows us to
write the equation of state in its usual form
 |
(269) |
The above derivation of the ideal gas equation of state
is rather elegant. It is certainly far easier to
obtain the equation of state in this manner
than to treat the atoms which make up the
gas as little billiard balls
which continually
bounce of the walls of a container. The latter derivation is difficult to
perform correctly because it is necessary
to average over all possible directions of
atomic motion. It is clear, from the above derivation, that the crucial element
needed to obtain the ideal gas equation of state is the absence of interatomic forces.
This automatically gives rise to a variation of the number of accessible states
with  and
and 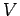 of
the form (6.6), which, in turn, implies the ideal gas law. So, the ideal gas law
should also apply to polyatomic gases with no interatomic forces. Polyatomic
gases are more complicated that monatomic gases because the molecules can rotate
and vibrate, giving rise to extra degrees of freedom, in addition to the
translational degrees of freedom of a monatomic gas. In other words,
of
the form (6.6), which, in turn, implies the ideal gas law. So, the ideal gas law
should also apply to polyatomic gases with no interatomic forces. Polyatomic
gases are more complicated that monatomic gases because the molecules can rotate
and vibrate, giving rise to extra degrees of freedom, in addition to the
translational degrees of freedom of a monatomic gas. In other words,
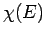 , in Eq. (265), becomes a lot more complicated
in polyatomic gases. However, as long as there
are no interatomic forces, the volume dependence of
, in Eq. (265), becomes a lot more complicated
in polyatomic gases. However, as long as there
are no interatomic forces, the volume dependence of  is still
is still 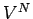 , and the
ideal gas law should still hold true. In fact, we
shall discover that the extra degrees of freedom of polyatomic gases manifest
themselves by increasing the specific heat capacity.
, and the
ideal gas law should still hold true. In fact, we
shall discover that the extra degrees of freedom of polyatomic gases manifest
themselves by increasing the specific heat capacity.
There is one other conclusion we can draw from Eq. (265). The statistical
definition of temperature is [Eq. (187)]
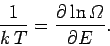 |
(270) |
It follows that
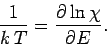 |
(271) |
We can see that since 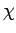 is a function of the energy, but not the volume,
then
the temperature must be a function of the
energy, but not the volume. We can turn this around and write
is a function of the energy, but not the volume,
then
the temperature must be a function of the
energy, but not the volume. We can turn this around and write
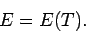 |
(272) |
In other words, the internal energy of an ideal gas depends only on the temperature
of the gas, and is independent of the volume.
This is pretty obvious, since if there are no interatomic forces
then increasing the volume, which
effectively increases the mean separation between molecules,
is not going to affect the molecular energies in any way. Hence, the energy of the
whole gas is unaffected.
The volume independence of the internal energy can also
be obtained directly from the ideal gas equation of state.
The internal energy of a gas can be considered as a general function of the
temperature and volume, so
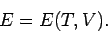 |
(273) |
It follows from mathematics that
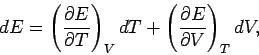 |
(274) |
where the subscript 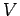 reminds us that the first partial derivative is taken
at constant volume, and the subscript
reminds us that the first partial derivative is taken
at constant volume, and the subscript  reminds us that the second
partial derivative
is taken at constant temperature. Thermodynamics tells us that for a quasi-static
change of parameters
reminds us that the second
partial derivative
is taken at constant temperature. Thermodynamics tells us that for a quasi-static
change of parameters
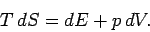 |
(275) |
The ideal gas law can be used to express the pressure in term of the volume and
the temperature in the above expression. Thus,
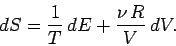 |
(276) |
Using Eq. (6.15), this becomes
![\begin{displaymath}
dS = \frac{1}{T} \left(\frac{\partial E}{\partial T}\right)_...
...partial E}{\partial V}\right)_T +
\frac{\nu\, R}{V}\right] dV.
\end{displaymath}](img738.png) |
(277) |
However, 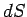 is the exact differential of a well-defined state function,
is the exact differential of a well-defined state function,
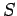 .
This means that we can consider the entropy to be a function of temperature and
volume. Thus,
.
This means that we can consider the entropy to be a function of temperature and
volume. Thus, 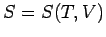 , and mathematics immediately tells us that
, and mathematics immediately tells us that
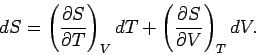 |
(278) |
The above expression is true for all small values of  and
and 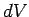 , so a comparison
with Eq. (277) gives
, so a comparison
with Eq. (277) gives
One well-known property of partial differentials is the equality of second
derivatives, irrespective of the order of differentiation, so
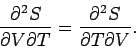 |
(281) |
This implies that
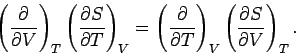 |
(282) |
The above expression can be combined with Eqs. (279) and
(280) to give
![\begin{displaymath}
\frac{1}{T} \left(\frac{\partial ^2 E}{\partial V \partial T...
...eft (\frac{\partial^2 E}{\partial T \partial V}\right)\right].
\end{displaymath}](img748.png) |
(283) |
Since second derivatives are equivalent, irrespective of the order of
differentiation,
the above relation reduces to
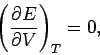 |
(284) |
which implies that the internal energy is independent of the volume for any gas obeying
the ideal equation of state. This result
was confirmed experimentally by James Joule in
the middle of the nineteenth century.



Next: Heat capacity or specific
Up: Classical thermodynamics
Previous: Introduction
Richard Fitzpatrick
2006-02-02
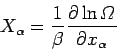
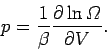
![]() and
and ![]() of
the form (6.6), which, in turn, implies the ideal gas law. So, the ideal gas law
should also apply to polyatomic gases with no interatomic forces. Polyatomic
gases are more complicated that monatomic gases because the molecules can rotate
and vibrate, giving rise to extra degrees of freedom, in addition to the
translational degrees of freedom of a monatomic gas. In other words,
of
the form (6.6), which, in turn, implies the ideal gas law. So, the ideal gas law
should also apply to polyatomic gases with no interatomic forces. Polyatomic
gases are more complicated that monatomic gases because the molecules can rotate
and vibrate, giving rise to extra degrees of freedom, in addition to the
translational degrees of freedom of a monatomic gas. In other words,
![]() , in Eq. (265), becomes a lot more complicated
in polyatomic gases. However, as long as there
are no interatomic forces, the volume dependence of
, in Eq. (265), becomes a lot more complicated
in polyatomic gases. However, as long as there
are no interatomic forces, the volume dependence of ![]() is still
is still ![]() , and the
ideal gas law should still hold true. In fact, we
shall discover that the extra degrees of freedom of polyatomic gases manifest
themselves by increasing the specific heat capacity.
, and the
ideal gas law should still hold true. In fact, we
shall discover that the extra degrees of freedom of polyatomic gases manifest
themselves by increasing the specific heat capacity.
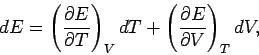
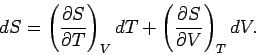
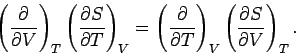
![\begin{displaymath}
\frac{1}{T} \left(\frac{\partial ^2 E}{\partial V \partial T...
...eft (\frac{\partial^2 E}{\partial T \partial V}\right)\right].
\end{displaymath}](img748.png)