


Next: Heat and work
Up: Statistical mechanics
Previous: Probability calculations
Behaviour of the density of states
Consider an
isolated system in equilibrium whose volume is 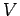 , and whose energy lies in the
range
, and whose energy lies in the
range  to
to  .
Let
.
Let
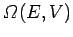 be the total number of microscopic states which
satisfy these constraints.
It would be useful if we could estimate how
this number typically varies with the macroscopic parameters of the system.
The easiest way to do this is to consider a specific example. For instance,
an ideal gas made up of spinless monatomic particles. This is a particularly
simple example,
because for such a gas the particles possess translational but no
internal (e.g., vibrational, rotational, or spin) degrees of freedom.
By definition, interatomic forces are negligible in an ideal gas. In other
words, the individual particles
move in an approximately uniform potential.
It follows that the energy of the gas is just
the total translational kinetic energy of its constituent particles. Thus,
be the total number of microscopic states which
satisfy these constraints.
It would be useful if we could estimate how
this number typically varies with the macroscopic parameters of the system.
The easiest way to do this is to consider a specific example. For instance,
an ideal gas made up of spinless monatomic particles. This is a particularly
simple example,
because for such a gas the particles possess translational but no
internal (e.g., vibrational, rotational, or spin) degrees of freedom.
By definition, interatomic forces are negligible in an ideal gas. In other
words, the individual particles
move in an approximately uniform potential.
It follows that the energy of the gas is just
the total translational kinetic energy of its constituent particles. Thus,
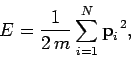 |
(104) |
where  is the particle mass,
is the particle mass,  the total number of particles,
and
the total number of particles,
and 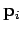 the
vector momentum of the
the
vector momentum of the 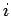 th particle.
th particle.
Consider the system in the
limit in which the energy  of the gas is
much greater than the ground-state energy, so that all of the
quantum numbers are large.
The classical version of statistical mechanics, in which we
divide up phase-space into cells of equal volume, is valid in this limit.
The number of
states
of the gas is
much greater than the ground-state energy, so that all of the
quantum numbers are large.
The classical version of statistical mechanics, in which we
divide up phase-space into cells of equal volume, is valid in this limit.
The number of
states
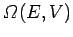 lying between the energies
lying between the energies  and
and  is simply
equal to the number of cells in phase-space contained between these energies.
In other words,
is simply
equal to the number of cells in phase-space contained between these energies.
In other words,
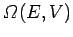 is proportional to the volume of
phase-space between these two energies:
is proportional to the volume of
phase-space between these two energies:
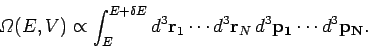 |
(105) |
Here, the integrand is the element of volume of phase-space, with
where  ,
, 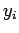 ,
, 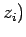 and
and  ,
, 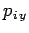 ,
, 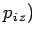 are the Cartesian coordinates and momentum components of the
are the Cartesian coordinates and momentum components of the 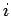 th particle,
respectively.
The integration is over all coordinates and momenta such that the total energy
of the system lies between
th particle,
respectively.
The integration is over all coordinates and momenta such that the total energy
of the system lies between  and
and  .
.
For an ideal gas, the total energy  does not depend on the positions of the
particles [see Eq. (104)]. This means that the integration over the
position vectors
does not depend on the positions of the
particles [see Eq. (104)]. This means that the integration over the
position vectors 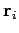 can be performed immediately. Since each integral over
can be performed immediately. Since each integral over 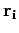 extends over
the volume of the container (the particles are, of course, not allowed to stray
outside the container),
extends over
the volume of the container (the particles are, of course, not allowed to stray
outside the container),
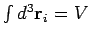 . There
are
. There
are  such integrals, so Eq. (105) reduces to
such integrals, so Eq. (105) reduces to
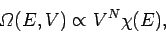 |
(108) |
where
 |
(109) |
is a momentum space integral which is independent of the volume.
The energy of the system can be written
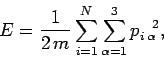 |
(110) |
since
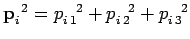 ,
denoting the
,
denoting the  ,
, 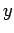 ,
,
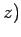 components by (1, 2, 3), respectively. The above sum contains
components by (1, 2, 3), respectively. The above sum contains 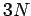 square terms.
For
square terms.
For 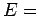 constant, Eq. (110) describes the locus of a
sphere of radius
constant, Eq. (110) describes the locus of a
sphere of radius
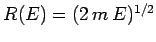 in
the
in
the 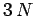 -dimensional space of the momentum components. Hence,
-dimensional space of the momentum components. Hence, 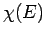 is
proportional to the volume of momentum phase-space contained in the spherical
shell lying between the sphere of radius
is
proportional to the volume of momentum phase-space contained in the spherical
shell lying between the sphere of radius 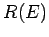 and that of slightly larger
radius
and that of slightly larger
radius 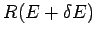 . This volume is
proportional to the area of the inner sphere multiplied by
. This volume is
proportional to the area of the inner sphere multiplied by
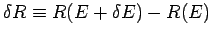 .
Since the area varies like
.
Since the area varies like  , and
, and
 ,
we have
,
we have
 |
(111) |
Combining this result with
(108) yields
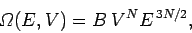 |
(112) |
where 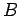 is a constant independent of
is a constant independent of 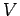 or
or  , and we have also
made use of
, and we have also
made use of 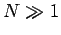 . Note that, since the number of degrees of freedom of the
system is
. Note that, since the number of degrees of freedom of the
system is 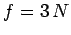 , the above relation can be very approximately written
, the above relation can be very approximately written
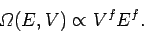 |
(113) |
In other words, the density of states varies like the extensive
macroscopic parameters of the system
raised to the power of the number of degrees of freedom. An extensive parameter is
one which scales with the size of the system (e.g., the volume).
Since thermodynamic
systems generally possess a very large number of degrees of freedom, this
result implies that the density of states
is an exceptionally rapidly increasing function of
the energy and volume.
This result, which turns out to be quite general, is very useful in statistical
thermodynamics.



Next: Heat and work
Up: Statistical mechanics
Previous: Probability calculations
Richard Fitzpatrick
2006-02-02
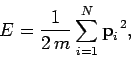
![]() of the gas is
much greater than the ground-state energy, so that all of the
quantum numbers are large.
The classical version of statistical mechanics, in which we
divide up phase-space into cells of equal volume, is valid in this limit.
The number of
states
of the gas is
much greater than the ground-state energy, so that all of the
quantum numbers are large.
The classical version of statistical mechanics, in which we
divide up phase-space into cells of equal volume, is valid in this limit.
The number of
states
![]() lying between the energies
lying between the energies ![]() and
and ![]() is simply
equal to the number of cells in phase-space contained between these energies.
In other words,
is simply
equal to the number of cells in phase-space contained between these energies.
In other words,
![]() is proportional to the volume of
phase-space between these two energies:
is proportional to the volume of
phase-space between these two energies:
![]() does not depend on the positions of the
particles [see Eq. (104)]. This means that the integration over the
position vectors
does not depend on the positions of the
particles [see Eq. (104)]. This means that the integration over the
position vectors ![]() can be performed immediately. Since each integral over
can be performed immediately. Since each integral over ![]() extends over
the volume of the container (the particles are, of course, not allowed to stray
outside the container),
extends over
the volume of the container (the particles are, of course, not allowed to stray
outside the container),
![]() . There
are
. There
are ![]() such integrals, so Eq. (105) reduces to
such integrals, so Eq. (105) reduces to