


Next: The equation of state
Up: Classical thermodynamics
Previous: Classical thermodynamics
We have learned that macroscopic quantities such as energy, temperature, and pressure
are, in fact, statistical in nature: i.e., in equilibrium they exhibit random
fluctuations about some mean value. If we were to plot out the probability
distribution for the energy, say, of a system in thermal equilibrium with its
surroundings we would obtain a Gaussian with a very small fractional width.
In fact, we expect
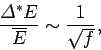 |
(260) |
where the number of degrees of freedom 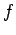 is about
is about 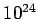 for laboratory
scale systems. This means that the statistical fluctuations of macroscopic
quantities about their mean values are typically only about 1 in
for laboratory
scale systems. This means that the statistical fluctuations of macroscopic
quantities about their mean values are typically only about 1 in 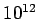 .
.
Since the statistical fluctuations of equilibrium quantities are so small, we can
neglect them to an excellent approximation, and replace macroscopic
quantities, such as energy, temperature, and pressure, by their mean
values. So,
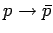 , and
, and
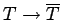 , etc.
In the following discussion, we shall drop the overbars altogether, so that
, etc.
In the following discussion, we shall drop the overbars altogether, so that 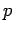 should
be understood to represent the mean pressure
should
be understood to represent the mean pressure 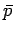 , etc. This
prescription, which is the essence of classical thermodynamics, is equivalent to
replacing all statistically varying quantities by their most probable values.
, etc. This
prescription, which is the essence of classical thermodynamics, is equivalent to
replacing all statistically varying quantities by their most probable values.
Although there are formally four laws of thermodynamics (i.e., the zeroth to the
third), the zeroth law is really a consequence of the second law, and the third
law is actually only important at temperatures close to absolute zero. So, for
most purposes, the two laws which really matter are the first law and the second law.
For an infinitesimal process, the first law is written
 |
(261) |
where 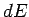 is the change in internal energy of the system,
is the change in internal energy of the system,
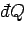 is the heat
absorbed by the system, and
is the heat
absorbed by the system, and
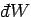 is the work done
by the system on its surroundings. Note that this is
just a convention. We could equally well write the first law in terms of the heat
emitted by the system or the work done on the system. It does not
really matter, as
long as we are consistent in our definitions.
is the work done
by the system on its surroundings. Note that this is
just a convention. We could equally well write the first law in terms of the heat
emitted by the system or the work done on the system. It does not
really matter, as
long as we are consistent in our definitions.
The second law of thermodynamics implies that
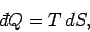 |
(262) |
for a quasi-static process,
where  is the thermodynamic temperature, and
is the thermodynamic temperature, and 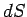 is the change in entropy of
the system. Furthermore, for systems in which the only external parameter is the
volume (i.e., gases),
the work done on the environment is
is the change in entropy of
the system. Furthermore, for systems in which the only external parameter is the
volume (i.e., gases),
the work done on the environment is
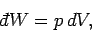 |
(263) |
where 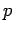 is the pressure, and
is the pressure, and 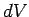 is the change in volume.
Thus, it follows from the first
and second laws of thermodynamics that
is the change in volume.
Thus, it follows from the first
and second laws of thermodynamics that
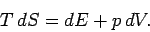 |
(264) |



Next: The equation of state
Up: Classical thermodynamics
Previous: Classical thermodynamics
Richard Fitzpatrick
2006-02-02
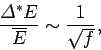
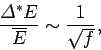
![]() , and
, and
![]() , etc.
In the following discussion, we shall drop the overbars altogether, so that
, etc.
In the following discussion, we shall drop the overbars altogether, so that ![]() should
be understood to represent the mean pressure
should
be understood to represent the mean pressure ![]() , etc. This
prescription, which is the essence of classical thermodynamics, is equivalent to
replacing all statistically varying quantities by their most probable values.
, etc. This
prescription, which is the essence of classical thermodynamics, is equivalent to
replacing all statistically varying quantities by their most probable values.