Next: Torque Balance Up: Error-Field Penetration in Tokamak Previous: Asymptotic Matching Contents
In the diffusive-resistive response regime (see Section 5.9),
where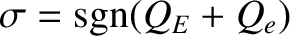 , and
, and
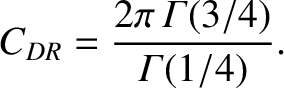 |
(7.12) |
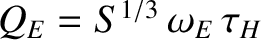 and
and
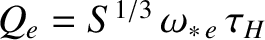 , where
, where
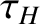 is the hydromagnetic timescale [see Equation (5.43)],
is the hydromagnetic timescale [see Equation (5.43)], 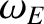 the E-cross-B frequency [see Equation (5.44)], and
the E-cross-B frequency [see Equation (5.44)], and
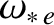 the electron diamagnetic frequency [see Equation (5.45)].
All quantities are evaluated at the rational surface. Moreover,
the electron diamagnetic frequency [see Equation (5.45)].
All quantities are evaluated at the rational surface. Moreover,
 and
and
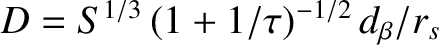 , where
, where
 is the resistive diffusion timescale [see Equation (5.49)],
is the resistive diffusion timescale [see Equation (5.49)],
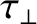 the energy confinement timescale [see Equation (5.52)],
the energy confinement timescale [see Equation (5.52)],
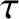 the ratio of the electron to the ion pressure gradient [see Equation (4.5)], and
the ratio of the electron to the ion pressure gradient [see Equation (4.5)], and
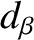 the ion sound radius [see Equation (4.75)]. In writing expression (7.11), we have made use of the fact that
the ion sound radius [see Equation (4.75)]. In writing expression (7.11), we have made use of the fact that
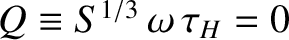 for a static magnetic perturbation.
for a static magnetic perturbation.
In the viscous-inertial response regime (see Section 5.11),
 |
(7.13) |
 |
(7.14) |
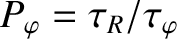 , where
, where
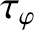 is the momentum confinement
timescale [see Equation (5.50)].
is the momentum confinement
timescale [see Equation (5.50)].
![\includegraphics[width=1.\textwidth]{Chapter07/Figure7_1.eps}](img2520.png)
|
Interpolating between the diffusive-resistive and the viscous-inertial response regimes, we can write
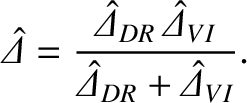 |
(7.15) |
Figure 7.1 shows the real and imaginary components of
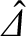 , as functions of the normalized E-cross-B frequency at the rational surface,
, as functions of the normalized E-cross-B frequency at the rational surface, 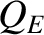 , calculated from Equations (7.16)–(7.18) for a low-field tokamak fusion reactor. The calculation
parameters are
, calculated from Equations (7.16)–(7.18) for a low-field tokamak fusion reactor. The calculation
parameters are 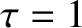 ,
,
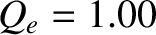 ,
, 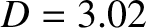 ,
,
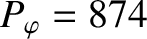 , and
, and
 . (See Table 5.1.)
If we compare Figure 7.1 with the exact numerical result shown in Figure 5.5 then we can see that the
analytic approximation (7.16)–(7.18) captures most of the salient features of the layer response. In particular, if we had tried to model the layer response just using either the diffusive-resistive or the viscous-inertial response regimes alone then the agreement with the numerical results would have been very poor. The
diffusive-resistive response regime predicts that
. (See Table 5.1.)
If we compare Figure 7.1 with the exact numerical result shown in Figure 5.5 then we can see that the
analytic approximation (7.16)–(7.18) captures most of the salient features of the layer response. In particular, if we had tried to model the layer response just using either the diffusive-resistive or the viscous-inertial response regimes alone then the agreement with the numerical results would have been very poor. The
diffusive-resistive response regime predicts that
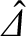 is purely imaginary, and that
is purely imaginary, and that
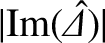 is a monotonically increasing function of
is a monotonically increasing function of  . On the other hand, the
viscous-inertial response regime does not predict a resonance (i.e., a point where
. On the other hand, the
viscous-inertial response regime does not predict a resonance (i.e., a point where
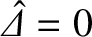 )
at
)
at  (i.e., when the electron fluid at the rational surface is stationary). Neither of these prediction are consistent with the data shown in Figure 5.5. Thus, it is clear that, in order to be reasonably accurate, an analytical approximation to the layer response must interpolate between
a constant-
(i.e., when the electron fluid at the rational surface is stationary). Neither of these prediction are consistent with the data shown in Figure 5.5. Thus, it is clear that, in order to be reasonably accurate, an analytical approximation to the layer response must interpolate between
a constant- response regime (in this case, the diffusive-resistive) and a nonconstant-
response regime (in this case, the diffusive-resistive) and a nonconstant- response regime (in this case, the
viscous-inertial).
response regime (in this case, the
viscous-inertial).
We saw in Section 5.13 that the relevant linear resonant response regimes in a high-field tokamak fusion reactor are the viscous-resistive and the viscous-inertial.
In the viscous-resistive response regime (see Section 5.9),
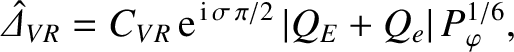 |
(7.19) |
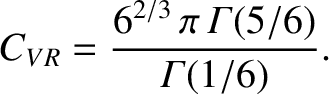 |
(7.20) |
Interpolating between the viscous-resistive and the viscous-inertial response regimes, we can write
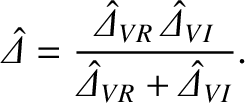 |
(7.21) |
![\includegraphics[width=1.\textwidth]{Chapter07/Figure7_2.eps}](img2538.png)
|
Figure 7.2 shows the real and imaginary components of
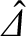 , as functions of the normalized E-cross-B frequency at the rational surface,
, as functions of the normalized E-cross-B frequency at the rational surface, 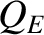 , calculated from Equations (7.22)–(7.24) for a high-field tokamak fusion reactor. The calculation
parameters are
, calculated from Equations (7.22)–(7.24) for a high-field tokamak fusion reactor. The calculation
parameters are
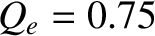 , and
, and
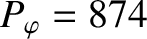 . (See Table 5.1.)
As before, if we compare Figure 7.2 with the exact numerical result shown in Figure 5.6 then we can see that the
analytic approximation (7.22)–(7.24) captures most of the salient features of the layer response.
. (See Table 5.1.)
As before, if we compare Figure 7.2 with the exact numerical result shown in Figure 5.6 then we can see that the
analytic approximation (7.22)–(7.24) captures most of the salient features of the layer response.