Next: Bibliography Up: Reduced Resonant Response Model Previous: Reduction Process Contents
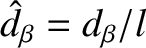 . Note that Equations (4.69)–(4.74) contain the physics of the shear-Alfvén and parallel ion sound waves, but do not contain the physics of the
compressible-Alfvén wave.
. Note that Equations (4.69)–(4.74) contain the physics of the shear-Alfvén and parallel ion sound waves, but do not contain the physics of the
compressible-Alfvén wave.
Equations (4.69)–(4.74) constitute our reduced drift-MHD resonant plasma response model. Our model is very similar
to the so-called four-field model derived by Hazeltine, et alia [7]. Equation (4.69) is the generalized
Ohm's law that governs the time evolution of the (normalized) helical magnetic flux, 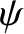 . [Note that this
. [Note that this 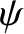 should not be confused with the equilibrium
poloidal flux defined in Equation (2.124).] Equation (4.70) is the energy equation that
governs the time evolution of the (normalized) perturbed total plasma pressure,
should not be confused with the equilibrium
poloidal flux defined in Equation (2.124).] Equation (4.70) is the energy equation that
governs the time evolution of the (normalized) perturbed total plasma pressure, 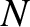 . Equation (4.71) is the ion parallel vorticity equation that governs the time evolution of the (normalized) ion parallel vorticity,
. Equation (4.71) is the ion parallel vorticity equation that governs the time evolution of the (normalized) ion parallel vorticity, 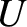 .
Finally, Equation (4.72) is the
ion parallel equation of motion that governs the time evolution of the (normalized) ion parallel velocity,
.
Finally, Equation (4.72) is the
ion parallel equation of motion that governs the time evolution of the (normalized) ion parallel velocity, 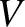 .
.
Strictly speaking, the reduced resonant response model derived in this chapter is only valid when the ion gyro-radius is smaller than the typical radial variation lengthscale in the resonant layer. If this is not the case then it is necessary to adopt a so-called gyro-fluid approach in which the ion response is averaged over the ion gyro-orbits [1,6,11].
Finally, the crucial element of the reduction process, by which our original drift-MHD response model is converted into a
reduced drift-MHD model, is the set of ordering assumptions that render
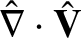 a second-order quantity while leaving
a second-order quantity while leaving
 a first-order quantity. This ordering implies that the MHD fluid is
incompressible to lowest order. (See Section 3.6.) It should be noted, however, that the small, but finite, compressibility of the
MHD fluid has a significant influence on the form of the energy equation (4.70).
a first-order quantity. This ordering implies that the MHD fluid is
incompressible to lowest order. (See Section 3.6.) It should be noted, however, that the small, but finite, compressibility of the
MHD fluid has a significant influence on the form of the energy equation (4.70).