Nonconstant- Linear Resonant Response Regimes
Linear Resonant Response Regimes
Suppose that
 and
and
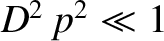 . It follows that
. It follows that  ,
, 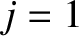 ,
, 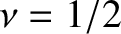 , and
, and
![$\displaystyle G = [-{\rm i}\,(Q-Q_E)]\,[-{\rm i}\,(Q-Q_E-Q_i)].$](img2232.png) |
(5.103) |
Hence, we deduce that
![$\displaystyle \skew{6}\hat{\mit\Delta} = -\frac{\pi}{[-{\rm i}\,(Q-Q_E)]^{1/2}\,[-{\rm i}\,(Q-Q_E-Q_i)]^{1/2}}.$](img2233.png) |
(5.104) |
This response regime is known as the inertial regime, because the layer response is dominated by
ion inertia [2,13]. Note that the plasma response in the inertial regime is
equivalent to that of two closely-spaced shear-Alfvén resonances that straddle the rational surface [4].
In fact, it is easily demonstrated that in real space,
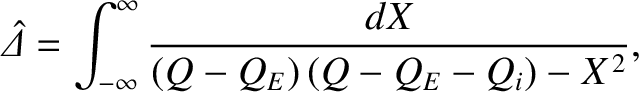 |
(5.105) |
which suggests that the resonances lie at
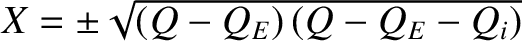 .
The characteristic layer width is
.
The characteristic layer width is
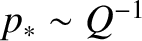 ,
which implies that the regime is valid when
,
which implies that the regime is valid when  ,
, 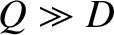 ,
, 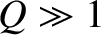 , and
, and
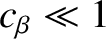 .
.
Suppose that
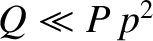 and
and
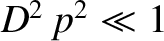 . It follows that
. It follows that 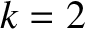 ,
, 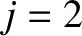 ,
,  , and
, and
![$\displaystyle G = [-{\rm i}\,(Q-Q_E-Q_e)]\,P_\varphi.$](img2241.png) |
(5.106) |
Hence, we deduce that
![$\displaystyle \skew{6}\hat{\mit\Delta} =- \frac{\pi}{2}\,\frac{{\mit\Gamma}(1/4)}{{\mit\Gamma}(3/4)}\, [-{\rm i}\,(Q-Q_E-Q_e)]^{-1/4}\,P_\varphi^{-1/4}.$](img2242.png) |
(5.107) |
This response regime is known as the viscous-inertial regime, because the layer response is dominated by
ion perpendicular viscosity and ion inertia [13].
The characteristic layer width is
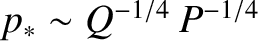 ,
which implies that the regime is valid when
,
which implies that the regime is valid when 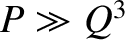 ,
,
 ,
,
 , and
, and
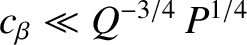 .
.
Suppose, finally, that
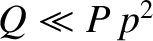 and
and
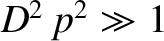 . It follows that
. It follows that  ,
, 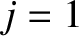 ,
, 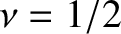 , and
, and
![$\displaystyle G = \frac{[-{\rm i}\,(Q-Q_E-Q_e)]\,P_\perp}{(1+1/\tau)\,D^2}.$](img2248.png) |
(5.108) |
Hence, we deduce that
![$\displaystyle \skew{6}\hat{\mit\Delta}= -\frac{\pi\,(1+1/\tau)^{1/2}\,D}{[-{\rm i}\,(Q-Q_E-\,Q_e)]^{1/2}\,P_\perp^{1/2}}.$](img2249.png) |
(5.109) |
This response regime is known as the diffusive-inertial regime, because the
layer response is dominated by perpendicular energy diffusivity and ion inertia [15]. The characteristic layer width is
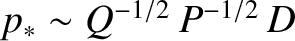 , which implies that the regime is valid when
, which implies that the regime is valid when 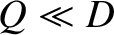 ,
,
 ,
,
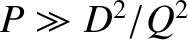 , and
, and
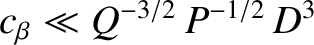 .
.
 Linear Resonant Response Regimes
Linear Resonant Response Regimes
 and
and
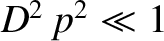 . It follows that
. It follows that  ,
, 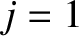 ,
, 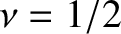 , and
, and
![$\displaystyle G = [-{\rm i}\,(Q-Q_E)]\,[-{\rm i}\,(Q-Q_E-Q_i)].$](img2232.png)
![$\displaystyle \skew{6}\hat{\mit\Delta} = -\frac{\pi}{[-{\rm i}\,(Q-Q_E)]^{1/2}\,[-{\rm i}\,(Q-Q_E-Q_i)]^{1/2}}.$](img2233.png)
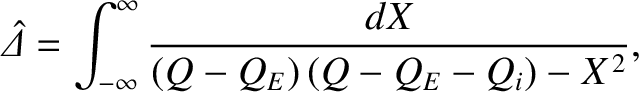
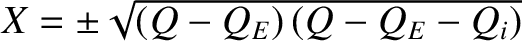 .
The characteristic layer width is
.
The characteristic layer width is
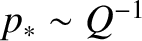 ,
which implies that the regime is valid when
,
which implies that the regime is valid when  ,
, 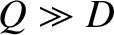 ,
, 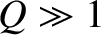 , and
, and
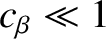 .
.
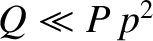 and
and
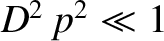 . It follows that
. It follows that 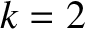 ,
, 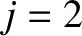 ,
,  , and
, and
![$\displaystyle G = [-{\rm i}\,(Q-Q_E-Q_e)]\,P_\varphi.$](img2241.png)
![$\displaystyle \skew{6}\hat{\mit\Delta} =- \frac{\pi}{2}\,\frac{{\mit\Gamma}(1/4)}{{\mit\Gamma}(3/4)}\, [-{\rm i}\,(Q-Q_E-Q_e)]^{-1/4}\,P_\varphi^{-1/4}.$](img2242.png)
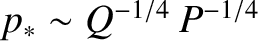 ,
which implies that the regime is valid when
,
which implies that the regime is valid when 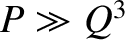 ,
,
 ,
,
 , and
, and
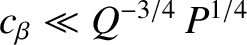 .
.
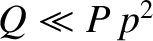 and
and
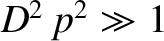 . It follows that
. It follows that  ,
, 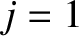 ,
, 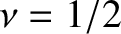 , and
, and
![$\displaystyle G = \frac{[-{\rm i}\,(Q-Q_E-Q_e)]\,P_\perp}{(1+1/\tau)\,D^2}.$](img2248.png)
![$\displaystyle \skew{6}\hat{\mit\Delta}= -\frac{\pi\,(1+1/\tau)^{1/2}\,D}{[-{\rm i}\,(Q-Q_E-\,Q_e)]^{1/2}\,P_\perp^{1/2}}.$](img2249.png)
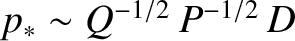 , which implies that the regime is valid when
, which implies that the regime is valid when 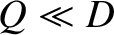 ,
,
 ,
,
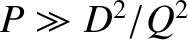 , and
, and
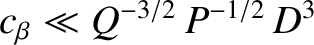 .
.