


Next: Asymptotic Series
Up: Wave Propagation in Inhomogeneous
Previous: Measurement of Ionospheric Electron
Suppose that we possess a radio antenna that is capable
of launching radio
waves of constant frequency  into the ionosphere at an angle to the vertical.
Let us consider the paths traced out by these waves in the
into the ionosphere at an angle to the vertical.
Let us consider the paths traced out by these waves in the
 -
- plane. For the
sake of simplicity, we shall assume that the waves are horizontally
polarized, so that the electric field vector always lies parallel to
the
plane. For the
sake of simplicity, we shall assume that the waves are horizontally
polarized, so that the electric field vector always lies parallel to
the 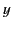 -axis. The signal emitted by the antenna (located at
-axis. The signal emitted by the antenna (located at 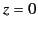 )
can be represented as
)
can be represented as
 |
(1138) |
where
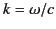 . Here, the
. Here, the
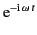 time dependence of
the signal has been neglected for the sake of clarity. Suppose that the signal emitted by
the antenna is mostly concentrated in a direction making an angle
time dependence of
the signal has been neglected for the sake of clarity. Suppose that the signal emitted by
the antenna is mostly concentrated in a direction making an angle 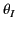 with the vertical. It follows that
with the vertical. It follows that 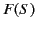 possesses a narrow maximum around
possesses a narrow maximum around
 , where
, where
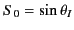 .
.
If Equation (1140) represents the signal at ground level then the signal
at height  in the ionosphere is easily obtained by making use of
the WKB solution for horizontally polarized waves
described in
Section 8.9. We obtain
in the ionosphere is easily obtained by making use of
the WKB solution for horizontally polarized waves
described in
Section 8.9. We obtain
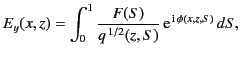 |
(1139) |
where
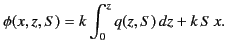 |
(1140) |
Equation (1141) is essentially a contour integral in  -space. The quantity
-space. The quantity
 is
a relatively slowly varying function of
is
a relatively slowly varying function of  , whereas the phase
, whereas the phase 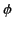 is a
large and rapidly varying function of
is a
large and rapidly varying function of  . As described in Section 7.12, the
rapid oscillations of
. As described in Section 7.12, the
rapid oscillations of
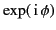 over most of the path
of integration ensure that the integrand averages almost to zero. In fact,
only those points on the path of integration where the phase is
stationary (i.e., where
over most of the path
of integration ensure that the integrand averages almost to zero. In fact,
only those points on the path of integration where the phase is
stationary (i.e., where
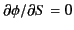 ) make a
significant contribution to the integral. It follows that the left-hand
side of Equation (1141) averages to a very small value, except for those
special values of
) make a
significant contribution to the integral. It follows that the left-hand
side of Equation (1141) averages to a very small value, except for those
special values of  and
and  at which one of the points of stationary
phase in
at which one of the points of stationary
phase in  -space coincides with the peak of
-space coincides with the peak of 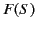 . The locus of
these special values of
. The locus of
these special values of  and
and  can clearly be regarded as the trajectory
of the radio signal emitted by the antenna as it passes through the
ionosphere. Thus, the signal trajectory is specified by
can clearly be regarded as the trajectory
of the radio signal emitted by the antenna as it passes through the
ionosphere. Thus, the signal trajectory is specified by
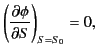 |
(1141) |
which yields
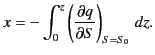 |
(1142) |
We can think of
this equation as tracing the path of a ray of radio frequency radiation,
emitted by the antenna at an angle 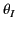 to the vertical (where
to the vertical (where
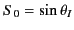 ), as it propagates through the ionosphere.
), as it propagates through the ionosphere.
Now
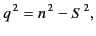 |
(1143) |
so the ray tracing equation becomes
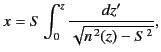 |
(1144) |
where  is the sine of the initial (i.e.,
at the antenna) angle of incidence of the
ray with respect to the vertical axis.
Of course, Equation (1146) only holds for upgoing rays. For downgoing
rays, a simple variant of the previous analysis using the downgoing WKB
solutions yields
is the sine of the initial (i.e.,
at the antenna) angle of incidence of the
ray with respect to the vertical axis.
Of course, Equation (1146) only holds for upgoing rays. For downgoing
rays, a simple variant of the previous analysis using the downgoing WKB
solutions yields
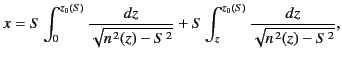 |
(1145) |
where
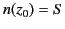 . Thus, the ray ascends into the ionosphere
after being launched from the antenna, reaches a maximum
height
. Thus, the ray ascends into the ionosphere
after being launched from the antenna, reaches a maximum
height 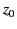 above the surface of the Earth, and then starts to
descend. The ray eventually intersects the Earth's surface again a horizontal
distance
above the surface of the Earth, and then starts to
descend. The ray eventually intersects the Earth's surface again a horizontal
distance
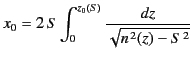 |
(1146) |
away from the antenna.
The angle 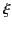 which the ray makes with the vertical is given by
which the ray makes with the vertical is given by
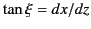 . It follows from Equations (1146) and (1147) that
. It follows from Equations (1146) and (1147) that
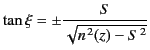 |
(1147) |
where the upper and lower signs correspond to the upgoing
and downgoing parts of the ray trajectory, respectively. Note that 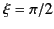 at the reflection point, where
at the reflection point, where 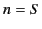 . Thus, the ray is horizontal at
the reflection point.
. Thus, the ray is horizontal at
the reflection point.
Let us investigate the reflection process in more detail.
In particular, we wish to demonstrate that radio waves are reflected at the 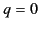 surface, rather than being absorbed. We would also like to understand the
origin of the
surface, rather than being absorbed. We would also like to understand the
origin of the  phase shift of radio waves at reflection which is evident
in Equation (1107).
In order to achieve
these goals, we shall need to review the mathematics of asymptotic series.
phase shift of radio waves at reflection which is evident
in Equation (1107).
In order to achieve
these goals, we shall need to review the mathematics of asymptotic series.



Next: Asymptotic Series
Up: Wave Propagation in Inhomogeneous
Previous: Measurement of Ionospheric Electron
Richard Fitzpatrick
2014-06-27

![]() in the ionosphere is easily obtained by making use of
the WKB solution for horizontally polarized waves
described in
Section 8.9. We obtain
in the ionosphere is easily obtained by making use of
the WKB solution for horizontally polarized waves
described in
Section 8.9. We obtain
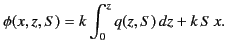
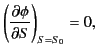
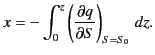
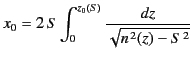
![]() which the ray makes with the vertical is given by
which the ray makes with the vertical is given by
![]() . It follows from Equations (1146) and (1147) that
. It follows from Equations (1146) and (1147) that
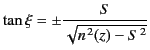
![]() surface, rather than being absorbed. We would also like to understand the
origin of the
surface, rather than being absorbed. We would also like to understand the
origin of the ![]() phase shift of radio waves at reflection which is evident
in Equation (1107).
In order to achieve
these goals, we shall need to review the mathematics of asymptotic series.
phase shift of radio waves at reflection which is evident
in Equation (1107).
In order to achieve
these goals, we shall need to review the mathematics of asymptotic series.