


Next: Exercises
Up: Electrostatic Fields
Previous: Boundary Value Problems
As an example of a boundary value problem, suppose that we wish to solve Poisson's equation, subject to Dirichlet boundary conditions, in some domain  that lies
between the spherical surfaces
that lies
between the spherical surfaces 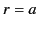 and
and 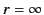 , where
, where 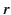 is a radial spherical coordinate. Let
is a radial spherical coordinate. Let  and
and 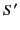 denote the former
and latter surfaces, respectively. The Green's function for the problem,
denote the former
and latter surfaces, respectively. The Green's function for the problem,
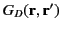 , must satisfy
, must satisfy
 |
(272) |
for  ,
, 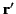 not outside
not outside  , and
, and
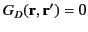 |
(273) |
when 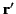 lies on
lies on  or on
or on 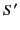 . The Green's function also has the symmetry property
. The Green's function also has the symmetry property
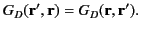 |
(274) |
Let us try
 |
(275) |
Note that the above function is symmetric with respect to its arguments, because
 .
It follows from Equation (25) that
.
It follows from Equation (25) that
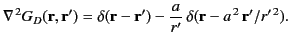 |
(276) |
However, if  ,
, 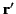 do not lie outside
do not lie outside  then the argument of the latter delta function cannot be zero.
Hence, for
then the argument of the latter delta function cannot be zero.
Hence, for  ,
, 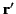 not outside
not outside  , this function takes the value zero, and the above expression reduces to
, this function takes the value zero, and the above expression reduces to
 |
(277) |
as required.
Equation (276) can be written
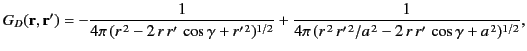 |
(278) |
where
 . When written in this form, it becomes clear that
. When written in this form, it becomes clear that
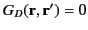 when
when 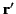 lies
on
lies
on  (i.e., when
(i.e., when 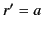 ) or on
) or on 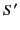 (i.e., when
(i.e., when 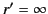 ). We conclude that expression (279) is the unique Green's function for the
Dirichlet problem within the domain
). We conclude that expression (279) is the unique Green's function for the
Dirichlet problem within the domain  .
.
According to Equation (246), the electrostatic potential within the domain  is written
is written
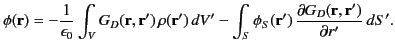 |
(279) |
Here,
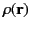 is the charge distribution within
is the charge distribution within  (i.e., the region
(i.e., the region 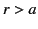 ),
),
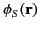 is the potential on
is the potential on  (i.e., the
surface
(i.e., the
surface 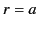 ), and the potential at infinity (i.e., on the surface
), and the potential at infinity (i.e., on the surface 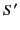 ) is assumed to be zero.
Moreover, we have made use of the fact that
) is assumed to be zero.
Moreover, we have made use of the fact that
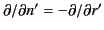 on
on  , because the unit vector
, because the unit vector  points radially inward. Finally,
it is easily demonstrated that
points radially inward. Finally,
it is easily demonstrated that
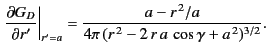 |
(280) |
Hence,
where 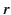 ,
, 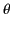 ,
, 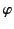 and
and  ,
, 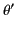 ,
,  are standard spherical coordinates, in terms of which,
are standard spherical coordinates, in terms of which,
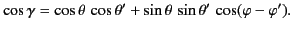 |
(282) |
As a specific example, suppose that  represents the surface of a grounded spherical conductor. It follows that
represents the surface of a grounded spherical conductor. It follows that 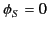 . Suppose that there
is a single charge,
. Suppose that there
is a single charge, 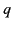 , in the domain
, in the domain  , located on the
, located on the  -axis at
-axis at 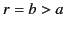 ,
,  , and
, and 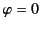 . It follows that
. It follows that
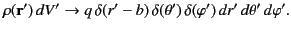 |
(283) |
Thus, Equations (282) and (283) yield
![$\displaystyle \phi(r,\theta) = \frac{q}{4\pi\,\epsilon_0}\left[\frac{1}{(r^{\,2...
...- \frac{1}{(r^{\,2}\,b^{\,2}/a^{\,2}-2\,r\,b\,\cos\theta+a^{\,2})^{1/2}}\right]$](img627.png) |
(284) |
in the region 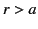 . Of course,
. Of course,  in the region
in the region 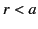 . It follows from Equations (154) and (203)
that there is a charge sheet on the surface of the conductor (because the normal electric field is non-zero just above the surface, but
zero just below) whose density is given by
. It follows from Equations (154) and (203)
that there is a charge sheet on the surface of the conductor (because the normal electric field is non-zero just above the surface, but
zero just below) whose density is given by
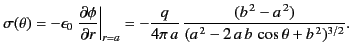 |
(285) |
Thus, the net charge induced on the surface of the conductor is
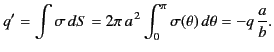 |
(286) |
In Equation (285), the first term inside the square brackets clearly represents the electric potential generated by the charge 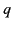 , which
suggests that
, which
suggests that
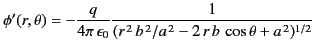 |
(287) |
is the potential generated by the charges induced on the surface of the conductor.
Hence, the attractive force acting on the charge 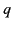 due to the induced charges is
due to the induced charges is
 |
(288) |
Of course, an equal and opposite force acts on the conductor.
As a final example, suppose that there are no charges in the domain  , but that
, but that 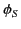 is prescribed on the surface
is prescribed on the surface  .
It follows from Equation (282) that the electric potential on the
.
It follows from Equation (282) that the electric potential on the  -axis (i.e.,
-axis (i.e., 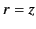 ,
,  , and
, and 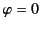 ) is
) is
 |
(289) |
for 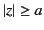 . Let
. Let  correspond to the surface of two conducting hemispheres (separated by a thin insulator). Suppose that
the upper (i.e.,
correspond to the surface of two conducting hemispheres (separated by a thin insulator). Suppose that
the upper (i.e.,
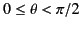 ) hemisphere is held at the potential
) hemisphere is held at the potential 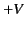 , whereas the lower (i.e.,
, whereas the lower (i.e.,
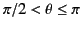 )
hemisphere is held at the potential
)
hemisphere is held at the potential 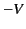 . It follows that
. It follows that
![$\displaystyle \phi(z) = \frac{V}{2}\,(z^{\,2}-a^{\,2})\,a\left[\int_0^1 \frac{d...
...2})^{3/2}}-\int_{-1}^0\frac{d\mu}{(z^{\,2}-2\,z\,a\,\mu+a^{\,2})^{3/2}}\right],$](img641.png) |
(290) |
where
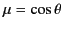 , which yields
, which yields
![$\displaystyle \phi(z) = {\rm sgn}(z)\,V\left[1-\frac{z^{\,2}-a^{\,2}}{\vert z\vert\,(z^{\,2}+a^{\,2})^{1/2}}\right]$](img643.png) |
(291) |
for 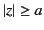 .
.



Next: Exercises
Up: Electrostatic Fields
Previous: Boundary Value Problems
Richard Fitzpatrick
2014-06-27
![]() is written
is written
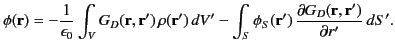
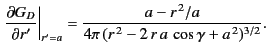
![]() represents the surface of a grounded spherical conductor. It follows that
represents the surface of a grounded spherical conductor. It follows that ![]() . Suppose that there
is a single charge,
. Suppose that there
is a single charge, ![]() , in the domain
, in the domain ![]() , located on the
, located on the ![]() -axis at
-axis at ![]() ,
, ![]() , and
, and ![]() . It follows that
. It follows that
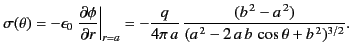
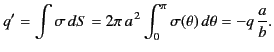
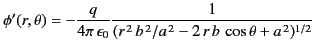

![]() , but that
, but that ![]() is prescribed on the surface
is prescribed on the surface ![]() .
It follows from Equation (282) that the electric potential on the
.
It follows from Equation (282) that the electric potential on the ![]() -axis (i.e.,
-axis (i.e., ![]() ,
, ![]() , and
, and ![]() ) is
) is

![$\displaystyle \phi(z) = \frac{V}{2}\,(z^{\,2}-a^{\,2})\,a\left[\int_0^1 \frac{d...
...2})^{3/2}}-\int_{-1}^0\frac{d\mu}{(z^{\,2}-2\,z\,a\,\mu+a^{\,2})^{3/2}}\right],$](img641.png)
![$\displaystyle \phi(z) = {\rm sgn}(z)\,V\left[1-\frac{z^{\,2}-a^{\,2}}{\vert z\vert\,(z^{\,2}+a^{\,2})^{1/2}}\right]$](img643.png)