


Next: Green's Theorem
Up: Electrostatic Fields
Previous: Electric Dipoles
Charge Sheets and Dipole Sheets
The electric potential due to a charge sheet (i.e., a charge distribution that is confined to a surface) can be obtained from Equation (162) by
replacing
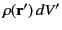 with
with
 . Here,
. Here,
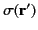 is the surface charge density (i.e., the charge per unit area) at position
is the surface charge density (i.e., the charge per unit area) at position 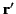 . We obtain
. We obtain
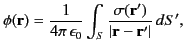 |
(202) |
where 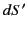 is an element of the surface
is an element of the surface  , on which the charges are distributed, located at position vector
, on which the charges are distributed, located at position vector 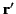 .
Incidentally, we are assuming that the
distribution is negligibly thin in the direction normal to the surface.
As is well known, application of Gauss' law to a thin pill-box aligned with an element of
.
Incidentally, we are assuming that the
distribution is negligibly thin in the direction normal to the surface.
As is well known, application of Gauss' law to a thin pill-box aligned with an element of  tells us that there is a discontinuity in the normal electric field across the sheet. In fact,
tells us that there is a discontinuity in the normal electric field across the sheet. In fact,
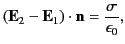 |
(203) |
where 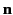 is a unit normal at a given point on the sheet,
is a unit normal at a given point on the sheet, 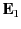 and
and 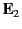 are the electric fields immediately to either side of the
sheet at this point (
are the electric fields immediately to either side of the
sheet at this point (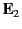 being the field on the side toward which
being the field on the side toward which 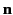 is directed), and
is directed), and  is the local charge density. As is
also well known, integration
of Equation (156) around a small loop that straddles the sheet reveals that there is no discontinuity in the tangential electric field
across the sheet.
is the local charge density. As is
also well known, integration
of Equation (156) around a small loop that straddles the sheet reveals that there is no discontinuity in the tangential electric field
across the sheet.
The electric potential due to a dipole sheet (i.e., a dipole distribution that is confined to a surface) can be obtained from Equation (201) by replacing
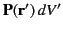 with
with
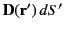 . Here,
. Here,
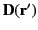 is the surface dipole density (i.e.,
the dipole moment per unit area) at position
is the surface dipole density (i.e.,
the dipole moment per unit area) at position 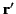 . We obtain
. We obtain
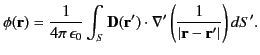 |
(204) |
We are again assuming that the distribution is negligibly thin in the direction normal to the surface  on which the dipoles
are distributed. Suppose that
on which the dipoles
are distributed. Suppose that
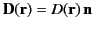 , where
, where 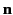 is a unit normal to the sheet at position vector
is a unit normal to the sheet at position vector  . In other words, suppose
that the constituent dipoles are all locally perpendicular to
. In other words, suppose
that the constituent dipoles are all locally perpendicular to  . It follows that
. It follows that
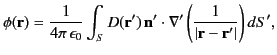 |
(205) |
where  is the unit normal to
is the unit normal to  at position
at position 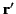 . Now, according to Equation (154) and (202), the normal electric field generated by a
charge sheet is
. Now, according to Equation (154) and (202), the normal electric field generated by a
charge sheet is
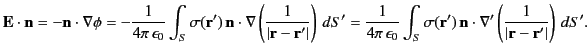 |
(206) |
A comparison between Equations (203), (205), and (206) reveals that there is
a discontinuity of the electric potential across a dipole sheet. In fact,
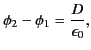 |
(207) |
where 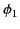 and
and 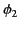 are the potentials immediately to either side of a given point on the
sheet [
are the potentials immediately to either side of a given point on the
sheet [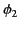 being the potential on the side toward which
being the potential on the side toward which 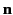 (and, hence,
(and, hence, 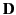 ) is directed], and
) is directed], and 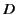 is the magnitude of the local dipole density.
[We can neglect the distinction between
is the magnitude of the local dipole density.
[We can neglect the distinction between  in Equation (205), and
in Equation (205), and 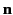 in Equation (206), because
the discontinuous part of the electric field due to a current sheet (as well as the discontinuous part of the potential due to a dipole sheet) is generated locally.]
Incidentally, there is no discontinuity in the normal electric field across a dipole sheet because the local charge density is zero.
Hence, although the potential is discontinuous across a dipole sheet, the normal derivative of the potential is continuous. Likewise, there
is no discontinuity in the electric potential across a charge sheet because the local dipole density is zero.
Thus, although the normal derivative of the potential is discontinuous across a charge sheet (because the normal electric field
is discontinuous), the potential itself is continuous.
in Equation (206), because
the discontinuous part of the electric field due to a current sheet (as well as the discontinuous part of the potential due to a dipole sheet) is generated locally.]
Incidentally, there is no discontinuity in the normal electric field across a dipole sheet because the local charge density is zero.
Hence, although the potential is discontinuous across a dipole sheet, the normal derivative of the potential is continuous. Likewise, there
is no discontinuity in the electric potential across a charge sheet because the local dipole density is zero.
Thus, although the normal derivative of the potential is discontinuous across a charge sheet (because the normal electric field
is discontinuous), the potential itself is continuous.
As an example, consider a charge sheet of uniform charge density  that corresponds to the plane
that corresponds to the plane 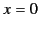 . Gauss' law,
in combination with symmetry arguments, reveals that
. Gauss' law,
in combination with symmetry arguments, reveals that
![$\displaystyle {\bf E} = \left\{ \begin{array}{rll} (\sigma/2\,\epsilon_0)\,{\bf...
...m}}& x>0\\ [0.5ex] - (\sigma/2\,\epsilon_0)\,{\bf e}_x&&x<0 \end{array}\right.,$](img487.png) |
(208) |
which is in accordance with Equation (203). It follows from Equation (154), and the requirement that the
electric potential be continuous across the sheet, that
![$\displaystyle \phi = \left\{ \begin{array}{rll} -(\sigma/2\,\epsilon_0)\,x&\mbo...
...space{0.5cm}}& x>0\\ [0.5ex] (\sigma/2\,\epsilon_0)\,x&&x<0 \end{array}\right..$](img488.png) |
(209) |
Consider, now, a dipole sheet of uniform dipole density
 that corresponds to the plane
that corresponds to the plane 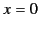 .
We can think of this sheet as a combination of two charge sheets: the first, of charge density
.
We can think of this sheet as a combination of two charge sheets: the first, of charge density  , located at
, located at
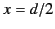 , and the second, of charge density
, and the second, of charge density 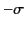 , located at
, located at  . In the limit
. In the limit
 , but
, but
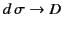 , the two charge sheets are equivalent to the dipole sheet. It follows, from the previous two
equations, that the electric field, and potential, generated by the dipole sheet are
, the two charge sheets are equivalent to the dipole sheet. It follows, from the previous two
equations, that the electric field, and potential, generated by the dipole sheet are
![$\displaystyle {\bf E} = \left\{ \begin{array}{rll} {\bf0}&\mbox{\hspace{0.5cm}}& x>0\\ [0.5ex] {\bf0}&&x<0 \end{array}\right.,$](img494.png) |
(210) |
and
![$\displaystyle \phi = \left\{ \begin{array}{rll} D/(2\,\epsilon_0)&\mbox{\hspace{0.5cm}}& x>0\\ [0.5ex] -D/(2\,\epsilon_0)&&x<0 \end{array}\right.,$](img495.png) |
(211) |
respectively. The latter equation is in accordance with Equation (207). Note that, although the dipole sheet does not
generated an external electric field, its internal field accelerates any charge that crosses the sheet. In fact, assuming that 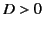 , a
positive charge gains energy by crossing the sheet from the region
, a
positive charge gains energy by crossing the sheet from the region  to the region
to the region  .
.
As a second example, consider a charge sheet of uniform charge density  that lies on the surface of a sphere, of radius
that lies on the surface of a sphere, of radius  ,
centered on the origin. Gauss' law,
in combination with symmetry arguments, reveals that
,
centered on the origin. Gauss' law,
in combination with symmetry arguments, reveals that
![$\displaystyle {\bf E} = \left\{ \begin{array}{lll} {\bf0}&\mbox{\hspace{0.5cm}}& r<a\\ [0.5ex] (\sigma/\epsilon_0)\,(a/r)^2\,{\bf e}_r &&r>a \end{array}\right.,$](img499.png) |
(212) |
where 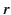 is a spherical polar coordinate.
The above expression is again in accordance with Equation (203). It follows from Equation (154), and the requirement that the
electric potential be continuous across the sheet (as well as zero at infinity), that
is a spherical polar coordinate.
The above expression is again in accordance with Equation (203). It follows from Equation (154), and the requirement that the
electric potential be continuous across the sheet (as well as zero at infinity), that
![$\displaystyle \phi = \left\{ \begin{array}{lll} \sigma\,a/\epsilon_0&\mbox{\hspace{0.5cm}}& r<a\\ [0.5ex] (\sigma\,a/\epsilon_0)\,(a/r)&&r>a \end{array}\right..$](img500.png) |
(213) |
Consider, now, a dipole sheet of uniform dipole density
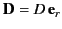 that lies on the surface of the sphere.
We can think of this sheet as a combination of two charge sheets: the first, of charge density
that lies on the surface of the sphere.
We can think of this sheet as a combination of two charge sheets: the first, of charge density
![$ \sigma\,[a/(a+d/2)]^{\,2}$](img502.png) , located at
, located at
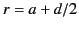 , and the second, of charge density
, and the second, of charge density
![$ -\sigma\,[a/(a-d/2)]^{\,2}$](img504.png) , located at
, located at 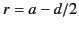 . (The
factors
. (The
factors
![$ [a/(a\pm d/2)]^{\,2}$](img506.png) are needed to ensure that both sheets contain equal and opposite net charge.) In the limit
are needed to ensure that both sheets contain equal and opposite net charge.) In the limit
 , but
, but
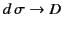 , the two charge sheets are equivalent to the dipole sheet.
It follows, from the previous two
equations, that the electric field, and potential, generated by the dipole sheet are
, the two charge sheets are equivalent to the dipole sheet.
It follows, from the previous two
equations, that the electric field, and potential, generated by the dipole sheet are
![$\displaystyle {\bf E} = \left\{ \begin{array}{rll} {\bf0}&\mbox{\hspace{0.5cm}}& r<a\\ [0.5ex] {\bf0}&&r>a \end{array}\right.,$](img507.png) |
(214) |
and
![$\displaystyle \phi = \left\{ \begin{array}{lll} -D/\epsilon_0&\mbox{\hspace{0.5cm}}& r<a\\ [0.5ex] 0&&r>a \end{array}\right.,$](img508.png) |
(215) |
respectively. The latter equation is in accordance with Equation (207). As before, the dipole sheet does not
generate an external electric field, but its internal field is capable of accelerating a charge that crosses the sheet.



Next: Green's Theorem
Up: Electrostatic Fields
Previous: Electric Dipoles
Richard Fitzpatrick
2014-06-27
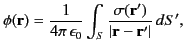
![]() with
with
![]() . Here,
. Here,
![]() is the surface dipole density (i.e.,
the dipole moment per unit area) at position
is the surface dipole density (i.e.,
the dipole moment per unit area) at position ![]() . We obtain
. We obtain
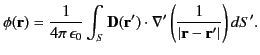
![]() that corresponds to the plane
that corresponds to the plane ![]() . Gauss' law,
in combination with symmetry arguments, reveals that
. Gauss' law,
in combination with symmetry arguments, reveals that
![$\displaystyle {\bf E} = \left\{ \begin{array}{rll} (\sigma/2\,\epsilon_0)\,{\bf...
...m}}& x>0\\ [0.5ex] - (\sigma/2\,\epsilon_0)\,{\bf e}_x&&x<0 \end{array}\right.,$](img487.png)
![$\displaystyle \phi = \left\{ \begin{array}{rll} -(\sigma/2\,\epsilon_0)\,x&\mbo...
...space{0.5cm}}& x>0\\ [0.5ex] (\sigma/2\,\epsilon_0)\,x&&x<0 \end{array}\right..$](img488.png)
![$\displaystyle {\bf E} = \left\{ \begin{array}{rll} {\bf0}&\mbox{\hspace{0.5cm}}& x>0\\ [0.5ex] {\bf0}&&x<0 \end{array}\right.,$](img494.png)
![$\displaystyle \phi = \left\{ \begin{array}{rll} D/(2\,\epsilon_0)&\mbox{\hspace{0.5cm}}& x>0\\ [0.5ex] -D/(2\,\epsilon_0)&&x<0 \end{array}\right.,$](img495.png)
![]() that lies on the surface of a sphere, of radius
that lies on the surface of a sphere, of radius ![]() ,
centered on the origin. Gauss' law,
in combination with symmetry arguments, reveals that
,
centered on the origin. Gauss' law,
in combination with symmetry arguments, reveals that
![$\displaystyle \phi = \left\{ \begin{array}{lll} \sigma\,a/\epsilon_0&\mbox{\hspace{0.5cm}}& r<a\\ [0.5ex] (\sigma\,a/\epsilon_0)\,(a/r)&&r>a \end{array}\right..$](img500.png)
![$\displaystyle {\bf E} = \left\{ \begin{array}{rll} {\bf0}&\mbox{\hspace{0.5cm}}& r<a\\ [0.5ex] {\bf0}&&r>a \end{array}\right.,$](img507.png)