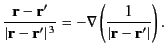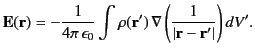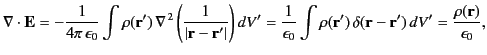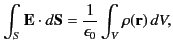Next: Electrostatic Energy
Up: Electrostatic Fields
Previous: Coulomb's Law
Electric Scalar Potential
It is easily demonstrated that
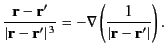 |
(153) |
Hence, Equation (152) yields
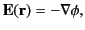 |
(154) |
where
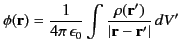 |
(155) |
is the scalar potential. (See Section 1.3.)
It follows from Equation (154) that
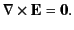 |
(156) |
In other words, an electric field generated by (stationary) charges is irrotational.
According to Equation (153), we can write Equation (152) in the form
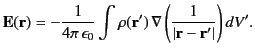 |
(157) |
Hence,
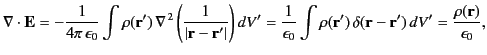 |
(158) |
where use has been made of Equations (23)-(25). We deduce that
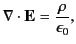 |
(159) |
which we recognize as the first Maxwell equation. (See Section 1.2.)
The integral form of this equation, which follows from the divergence theorem,
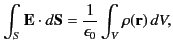 |
(160) |
is known as Gauss' law. Here,  is the bounding surface of volume
is the bounding surface of volume  .
.
Equations (154) and (159) can be combined to give
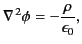 |
(161) |
which we recognize as Poisson's equation, with
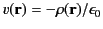 . (See Section 2.3.) Hence,
Equation (147) yields
. (See Section 2.3.) Hence,
Equation (147) yields
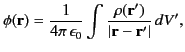 |
(162) |
which is equivalent to Equation (155). Incidentally, according to the analysis of Sections 2.2 and 2.3, the previous expression represents the unique solution to Equation (161), subject to the boundary condition
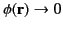 as as 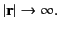 |
(163) |



Next: Electrostatic Energy
Up: Electrostatic Fields
Previous: Coulomb's Law
Richard Fitzpatrick
2014-06-27