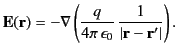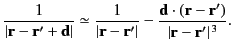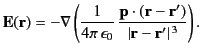Next: Charge Sheets and Dipole
Up: Electrostatic Fields
Previous: Electrostatic Energy
Electric Dipoles
Consider a charge  located at position vector
located at position vector 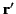 , and a charge
, and a charge 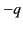 located at position vector
located at position vector
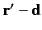 .
In the limit that
.
In the limit that
 , but
, but
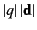 remains finite, this combination of charges constitutes an
electric dipole, of dipole moment
remains finite, this combination of charges constitutes an
electric dipole, of dipole moment
 |
(195) |
located at position vector 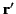 . We have seen that the electric field generated at point
. We have seen that the electric field generated at point  by an electric charge
by an electric charge 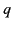 located
at point
located
at point 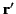 is
is
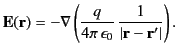 |
(196) |
Hence, the electric field generated at point  by an electric dipole of moment
by an electric dipole of moment 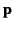 located at point
located at point 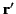 is
is
 |
(197) |
However, in the limit that
 ,
,
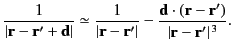 |
(198) |
Thus, the electric field due to the dipole becomes
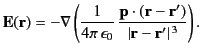 |
(199) |
It follows from Equation (154) that the scalar electric potential due to the dipole is
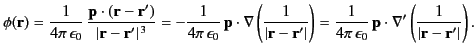 |
(200) |
(Here, 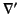 is a gradient operator expressed in terms of the components of
is a gradient operator expressed in terms of the components of 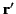 , but independent of the
components of
, but independent of the
components of  .)
Finally, because electric fields are superposable, the electric potential due to a volume distribution of electric dipoles
is
.)
Finally, because electric fields are superposable, the electric potential due to a volume distribution of electric dipoles
is
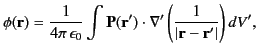 |
(201) |
where
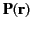 is the electric polarization (i.e., the electric dipole moment per unit volume), and
the integral is over all space.
is the electric polarization (i.e., the electric dipole moment per unit volume), and
the integral is over all space.



Next: Charge Sheets and Dipole
Up: Electrostatic Fields
Previous: Electrostatic Energy
Richard Fitzpatrick
2014-06-27