


Next: One-dimensional solution of Poisson's
Up: Electrostatics
Previous: Poisson's equation
We have already seen the great value of the uniqueness theorem for Poisson's
equation (or Laplace's equation) in our discussion of Helmholtz's theorem (see
Sect. 3.11). Let us now examine this theorem in detail.
Consider a volume  bounded by some surface
bounded by some surface  . Suppose that we are given
the charge density
. Suppose that we are given
the charge density 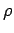 throughout
throughout  , and the value of the scalar potential
, and the value of the scalar potential
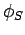 on
on  . Is this sufficient information to uniquely specify the scalar
potential throughout
. Is this sufficient information to uniquely specify the scalar
potential throughout  ? Suppose, for the sake of argument, that the
solution is not unique. Let there be two potentials
? Suppose, for the sake of argument, that the
solution is not unique. Let there be two potentials 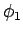 and
and 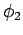 which
satisfy
which
satisfy
throughout  , and
, and
on  . We can form the difference between these two potentials:
. We can form the difference between these two potentials:
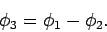 |
(670) |
The potential 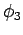 clearly satisfies
clearly satisfies
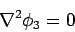 |
(671) |
throughout  , and
, and
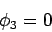 |
(672) |
on  .
.
According to vector field theory,
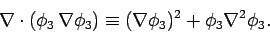 |
(673) |
Thus, using Gauss' theorem
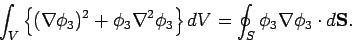 |
(674) |
But,
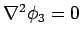 throughout
throughout  , and
, and 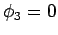 on
on  , so the
above equation reduces
to
, so the
above equation reduces
to
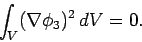 |
(675) |
Note that
 is a positive definite quantity. The only way in
which the volume integral of a positive definite quantity can be zero is if
that quantity itself is zero throughout the volume. This is not necessarily the
case for a non-positive definite quantity: we could have positive and negative
contributions from various regions inside the volume which cancel one another out.
Thus, since
is a positive definite quantity. The only way in
which the volume integral of a positive definite quantity can be zero is if
that quantity itself is zero throughout the volume. This is not necessarily the
case for a non-positive definite quantity: we could have positive and negative
contributions from various regions inside the volume which cancel one another out.
Thus, since
 is positive definite, it follows that
is positive definite, it follows that
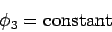 |
(676) |
throughout  . However, we know that
. However, we know that 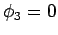 on
on  , so we get
, so we get
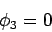 |
(677) |
throughout  . In other words,
. In other words,
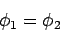 |
(678) |
throughout  and on
and on  . Our initial assumption that
. Our initial assumption that 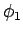 and
and 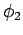 are two different solutions of Poisson's equation, satisfying the same
boundary conditions, turns out to be incorrect.
are two different solutions of Poisson's equation, satisfying the same
boundary conditions, turns out to be incorrect.
The fact that the solutions to Poisson's equation are unique is very useful.
It means that if we find a solution to this equation--no matter how contrived
the derivation--then this is the only possible solution. One immediate use of the
uniqueness theorem is to prove that the electric field inside an empty cavity
in a conductor is zero. Recall that our previous proof of this was rather involved,
and was also not particularly rigorous (see Sect. 5.4).
We know that the interior surface of the conductor is at some constant potential
 , say. So, we have
, say. So, we have 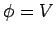 on the boundary of the cavity, and
on the boundary of the cavity, and
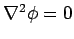 inside the cavity (since it contains no charges). One rather obvious
solution to these equations is
inside the cavity (since it contains no charges). One rather obvious
solution to these equations is 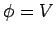 throughout the cavity. Since the
solutions to Poisson's equation are unique, this is the only solution.
Thus,
throughout the cavity. Since the
solutions to Poisson's equation are unique, this is the only solution.
Thus,
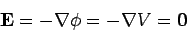 |
(679) |
inside the cavity.
Suppose that some volume  contains a number of conductors. We know that the
surface of each conductor is an equipotential surface, but, in general, we do not
know what potential each surface is at (unless we are specifically told that
it is earthed, etc.). However, if the conductors are insulated it is
plausible that we might know the charge on each conductor. Suppose that
there are
contains a number of conductors. We know that the
surface of each conductor is an equipotential surface, but, in general, we do not
know what potential each surface is at (unless we are specifically told that
it is earthed, etc.). However, if the conductors are insulated it is
plausible that we might know the charge on each conductor. Suppose that
there are 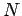 conductors, each carrying a charge
conductors, each carrying a charge 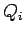 (
(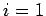 to
to 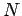 ), and suppose
that the region
), and suppose
that the region  containing these conductors is filled by a known charge
density
containing these conductors is filled by a known charge
density 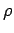 , and bounded by some surface
, and bounded by some surface  which is either infinity or
an enclosing conductor. Is this enough information to uniquely
specify the electric field throughout
which is either infinity or
an enclosing conductor. Is this enough information to uniquely
specify the electric field throughout  ?
?
Well, suppose that it is not enough information, so that there are two
fields 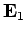 and
and 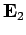 which satisfy
which satisfy
throughout  , with
, with
on the surface of the 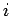 th conductor, and, finally,
th conductor, and, finally,
over the bounding surface,
where
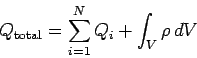 |
(686) |
is the total charge contained in volume  .
.
Let us form the difference field
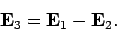 |
(687) |
It is clear that
 |
(688) |
throughout  , and
, and
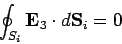 |
(689) |
for all 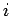 , with
, with
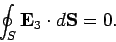 |
(690) |
Now, we know that each conductor is at a constant potential, so if
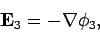 |
(691) |
then 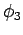 is a constant on the surface of each conductor. Furthermore,
if the outer surface
is a constant on the surface of each conductor. Furthermore,
if the outer surface  is infinity then
is infinity then
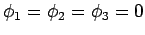 on this
surface. If the outer surface is an enclosing conductor then
on this
surface. If the outer surface is an enclosing conductor then 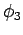 is
a constant on this surface. Either way,
is
a constant on this surface. Either way, 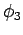 is constant on
is constant on  .
.
Consider the vector identity
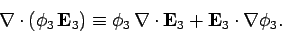 |
(692) |
We have
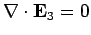 throughout
throughout  , and
, and
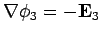 ,
so the above identity reduces to
,
so the above identity reduces to
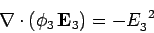 |
(693) |
throughout  . Integrating over
. Integrating over  , and making use of Gauss' theorem, yields
, and making use of Gauss' theorem, yields
 |
(694) |
However, 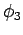 is a constant on the surfaces
is a constant on the surfaces 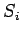 and
and  . So, making use of
Eqs. (689) and (690), we obtain
. So, making use of
Eqs. (689) and (690), we obtain
 |
(695) |
Of course,  is a positive definite quantity, so the above relation
implies that
is a positive definite quantity, so the above relation
implies that
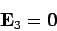 |
(696) |
throughout  : i.e., the fields
: i.e., the fields 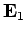 and
and 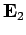 are
identical throughout
are
identical throughout  .
.
For a general electrostatic problem involving charges and
conductors, it is clear that if we are given either the potential at the surface of each conductor
or the charge carried by each conductor
(plus the charge density throughout the volume, etc.) then we can uniquely determine the electric
field. There are many other uniqueness theorems which generalize this result
still further: i.e., we could be given the potential of some of the conductors
and the charge carried by the others, and the solution would still be unique.
At this point, it is worth noting that there are also uniqueness theorems associated with
magnetostatics. For instance, if the current density, 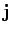 , is specified
throughout some volume
, is specified
throughout some volume  , and either the magnetic field,
, and either the magnetic field, 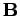 ,
or the vector potential,
,
or the vector potential,  , is specified on the bounding surface
, is specified on the bounding surface  , then
the magnetic field is uniquely determined throughout
, then
the magnetic field is uniquely determined throughout  and on
and on  .
The proof of this proposition proceeds along the usual lines. Suppose
that the magnetic field is not uniquely determined. In other words,
suppose there are two magnetic fields,
.
The proof of this proposition proceeds along the usual lines. Suppose
that the magnetic field is not uniquely determined. In other words,
suppose there are two magnetic fields, 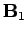 and
and 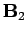 ,
satisfying
,
satisfying
throughout  . Suppose, further, that either
. Suppose, further, that either
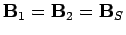 or
or
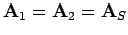 on
on  . Forming the
difference field,
. Forming the
difference field,
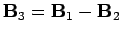 , we
have
, we
have
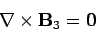 |
(699) |
throughout  , and either
, and either
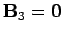 or
or
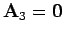 on
on  .
Now, according to vector field theory,
.
Now, according to vector field theory,
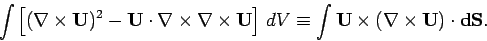 |
(700) |
Setting
 , and using
, and using
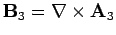 and Eq. (699), we obtain
and Eq. (699), we obtain
 |
(701) |
However, we know that either 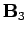 or
or 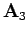 is zero on
is zero on  .
Hence, we obtain
.
Hence, we obtain
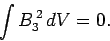 |
(702) |
Since,  is positive definite, the only way in which the above
equation can be satisfied is if
is positive definite, the only way in which the above
equation can be satisfied is if 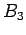 is zero throughout
is zero throughout  . Hence,
. Hence,
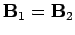 throughout
throughout  , and the solution is therefore unique.
, and the solution is therefore unique.



Next: One-dimensional solution of Poisson's
Up: Electrostatics
Previous: Poisson's equation
Richard Fitzpatrick
2006-02-02
![]() bounded by some surface
bounded by some surface ![]() . Suppose that we are given
the charge density
. Suppose that we are given
the charge density ![]() throughout
throughout ![]() , and the value of the scalar potential
, and the value of the scalar potential
![]() on
on ![]() . Is this sufficient information to uniquely specify the scalar
potential throughout
. Is this sufficient information to uniquely specify the scalar
potential throughout ![]() ? Suppose, for the sake of argument, that the
solution is not unique. Let there be two potentials
? Suppose, for the sake of argument, that the
solution is not unique. Let there be two potentials ![]() and
and ![]() which
satisfy
which
satisfy
![]() , say. So, we have
, say. So, we have ![]() on the boundary of the cavity, and
on the boundary of the cavity, and
![]() inside the cavity (since it contains no charges). One rather obvious
solution to these equations is
inside the cavity (since it contains no charges). One rather obvious
solution to these equations is ![]() throughout the cavity. Since the
solutions to Poisson's equation are unique, this is the only solution.
Thus,
throughout the cavity. Since the
solutions to Poisson's equation are unique, this is the only solution.
Thus,
![]() contains a number of conductors. We know that the
surface of each conductor is an equipotential surface, but, in general, we do not
know what potential each surface is at (unless we are specifically told that
it is earthed, etc.). However, if the conductors are insulated it is
plausible that we might know the charge on each conductor. Suppose that
there are
contains a number of conductors. We know that the
surface of each conductor is an equipotential surface, but, in general, we do not
know what potential each surface is at (unless we are specifically told that
it is earthed, etc.). However, if the conductors are insulated it is
plausible that we might know the charge on each conductor. Suppose that
there are ![]() conductors, each carrying a charge
conductors, each carrying a charge ![]() (
(![]() to
to ![]() ), and suppose
that the region
), and suppose
that the region ![]() containing these conductors is filled by a known charge
density
containing these conductors is filled by a known charge
density ![]() , and bounded by some surface
, and bounded by some surface ![]() which is either infinity or
an enclosing conductor. Is this enough information to uniquely
specify the electric field throughout
which is either infinity or
an enclosing conductor. Is this enough information to uniquely
specify the electric field throughout ![]() ?
?
![]() and
and ![]() which satisfy
which satisfy
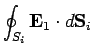
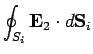
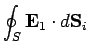
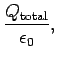


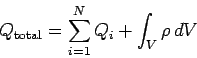

![]() , is specified
throughout some volume
, is specified
throughout some volume ![]() , and either the magnetic field,
, and either the magnetic field, ![]() ,
or the vector potential,
,
or the vector potential, ![]() , is specified on the bounding surface
, is specified on the bounding surface ![]() , then
the magnetic field is uniquely determined throughout
, then
the magnetic field is uniquely determined throughout ![]() and on
and on ![]() .
The proof of this proposition proceeds along the usual lines. Suppose
that the magnetic field is not uniquely determined. In other words,
suppose there are two magnetic fields,
.
The proof of this proposition proceeds along the usual lines. Suppose
that the magnetic field is not uniquely determined. In other words,
suppose there are two magnetic fields, ![]() and
and ![]() ,
satisfying
,
satisfying