


Next: The method of images
Up: Electrostatics
Previous: The uniqueness theorem
So, how do we actually solve Poisson's equation,
 |
(703) |
in practice? In general, the answer is that we use a computer. However, there
are a few situations, possessing a high degree of symmetry, where it is possible
to find analytic solutions. Let us discuss some of these solutions.
Suppose, first of all, that there is no variation of quantities in (say) the  - and
- and  -directions.
In this case, Poisson's equation reduces to an ordinary differential equation in
-directions.
In this case, Poisson's equation reduces to an ordinary differential equation in  ,
the solution of which is relatively straight-forward. Consider, for instance, a vacuum diode,
in which electrons are emitted from a hot cathode and accelerated towards an
anode, which is held at a large positive potential
,
the solution of which is relatively straight-forward. Consider, for instance, a vacuum diode,
in which electrons are emitted from a hot cathode and accelerated towards an
anode, which is held at a large positive potential 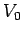 with respect to the
cathode. We can think of this as an essentially one-dimensional problem. Suppose
that the cathode is at
with respect to the
cathode. We can think of this as an essentially one-dimensional problem. Suppose
that the cathode is at 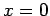 and the anode at
and the anode at  . Poisson's equation
takes the form
. Poisson's equation
takes the form
 |
(704) |
where  satisfies the boundary conditions
satisfies the boundary conditions  and
and  .
By energy conservation, an electron emitted from rest at the cathode
has an
.
By energy conservation, an electron emitted from rest at the cathode
has an  -velocity
-velocity  which satisfies
which satisfies
 |
(705) |
Finally, in a steady-state, the electric current 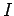 (between the anode and
cathode) is
independent of
(between the anode and
cathode) is
independent of  (otherwise, charge will build up at some points). In
fact,
(otherwise, charge will build up at some points). In
fact,
 |
(706) |
where 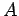 is the cross-sectional area of the diode.
The previous three equations can be combined to give
is the cross-sectional area of the diode.
The previous three equations can be combined to give
 |
(707) |
The solution of the above equation which satisfies the
boundary conditions is
 |
(708) |
with
 |
(709) |
This relationship between the current and the voltage in a vacuum diode is
called the Child-Langmuir law.
Let us now consider the solution of Poisson's equation in more than one
dimension.



Next: The method of images
Up: Electrostatics
Previous: The uniqueness theorem
Richard Fitzpatrick
2006-02-02


![]() - and
- and ![]() -directions.
In this case, Poisson's equation reduces to an ordinary differential equation in
-directions.
In this case, Poisson's equation reduces to an ordinary differential equation in ![]() ,
the solution of which is relatively straight-forward. Consider, for instance, a vacuum diode,
in which electrons are emitted from a hot cathode and accelerated towards an
anode, which is held at a large positive potential
,
the solution of which is relatively straight-forward. Consider, for instance, a vacuum diode,
in which electrons are emitted from a hot cathode and accelerated towards an
anode, which is held at a large positive potential ![]() with respect to the
cathode. We can think of this as an essentially one-dimensional problem. Suppose
that the cathode is at
with respect to the
cathode. We can think of this as an essentially one-dimensional problem. Suppose
that the cathode is at ![]() and the anode at
and the anode at ![]() . Poisson's equation
takes the form
. Poisson's equation
takes the form


