


Next: The uniqueness theorem
Up: Electrostatics
Previous: Capacitors
We know that in steady-state we can write
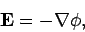 |
(663) |
with the scalar potential satisfying Poisson's equation:
 |
(664) |
We even know the general solution to this equation:
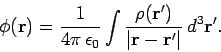 |
(665) |
So, what else is there to say about Poisson's equation? Well, consider a
positive (say) point
charge in the vicinity of an uncharged, insulated, conducting sphere. The charge
attracts negative charges to the near side of the sphere, and repels positive
charges to the far side. The surface charge distribution induced on the
sphere is such that it is maintained at a constant electrical potential.
We now have a problem. We cannot use formula (665) to work out the
potential 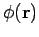 around the sphere, since we do not know how the
charges induced on the conducting surface are distributed. The only things
which we know about the surface of the sphere are that it is an equipotential surface,
and carries zero net charge. Clearly, in the presence of conducting surfaces the
solution (665) to Poisson's equation is completely useless. Let us now try to
develop some techniques for solving Poisson's equation which allow us to solve
real problems (which invariably involve conductors).
around the sphere, since we do not know how the
charges induced on the conducting surface are distributed. The only things
which we know about the surface of the sphere are that it is an equipotential surface,
and carries zero net charge. Clearly, in the presence of conducting surfaces the
solution (665) to Poisson's equation is completely useless. Let us now try to
develop some techniques for solving Poisson's equation which allow us to solve
real problems (which invariably involve conductors).



Next: The uniqueness theorem
Up: Electrostatics
Previous: Capacitors
Richard Fitzpatrick
2006-02-02