


Next: Boundary conditions on the
Up: Electrostatics
Previous: Ohm's law
Conductors
Most (but not all) electrical conductors obey Ohm's law. Such conductors are
termed ohmic.
Suppose that we apply an electric field to an ohmic conductor. What is going to
happen? According to Eq. (613), the electric field drives
currents. These redistribute the charge inside the conductor until the
original electric field is canceled out. At this point, the currents stop
flowing. It might be objected that the currents
could keep flowing in closed loops. According to Ohm's law, this would
require a non-zero e.m.f.,
 ,
acting around each loop (unless the conductor is a
superconductor, with
,
acting around each loop (unless the conductor is a
superconductor, with 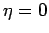 ). However, we know that in steady-state
). However, we know that in steady-state
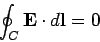 |
(617) |
around any closed loop  . This proves that a steady-state e.m.f. acting around
a closed loop inside a conductor is impossible. The only other alternative is
. This proves that a steady-state e.m.f. acting around
a closed loop inside a conductor is impossible. The only other alternative is
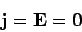 |
(618) |
inside a conductor. It immediately follows from the Maxwell equation,
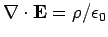 ,
that
,
that
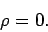 |
(619) |
So, there are no electric charges in the interior of a
conductor. But, how can a conductor cancel out an applied electric field
if it contains no charges? The answer is that all of the charges reside on the
surface of the conductor.
In reality, the charges lie
within one or two atomic layers of the surface (see any textbook on solid-state
physics).
The difference in scalar potential between
two points  and
and  is simply
is simply
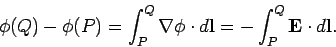 |
(620) |
However, if  and
and  lie inside the same conductor
then it is clear from Eq. (620) that the potential difference between
lie inside the same conductor
then it is clear from Eq. (620) that the potential difference between  and
and
 is zero. This is true no matter where
is zero. This is true no matter where  and
and  are situated inside the
conductor, so we conclude that the scalar potential must be
uniform inside a conductor.
A corollary of this is that the surface of a conductor is
an equipotential (i.e.,
are situated inside the
conductor, so we conclude that the scalar potential must be
uniform inside a conductor.
A corollary of this is that the surface of a conductor is
an equipotential (i.e., 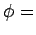 constant) surface.
constant) surface.
Figure 41:
 |
Not only is the electric field inside a conductor zero. It is also possible to
demonstrate that the field within an empty cavity lying inside a conductor is
also zero, provided that there are no charges within the cavity.
Let us, first of all, apply Gauss' law to a surface  which
surrounds the cavity, but lies
wholly in the conducting material (see Fig. 41). Since the electric field is zero in a conductor,
it follows that zero net charge is enclosed by
which
surrounds the cavity, but lies
wholly in the conducting material (see Fig. 41). Since the electric field is zero in a conductor,
it follows that zero net charge is enclosed by  . This does not preclude the
possibility that there are equal amounts of positive and negative charges distributed
on the inner surface of the conductor. However, we can easily rule out this
possibility using the steady-state relation
. This does not preclude the
possibility that there are equal amounts of positive and negative charges distributed
on the inner surface of the conductor. However, we can easily rule out this
possibility using the steady-state relation
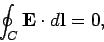 |
(621) |
for any closed loop  . If there are any electric field-lines inside the cavity
then
they must run from the positive to the negative surface charges. Consider a
loop
. If there are any electric field-lines inside the cavity
then
they must run from the positive to the negative surface charges. Consider a
loop  which straddles the cavity and the conductor, such as the one
shown in Fig. 41. In the presence of field-lines, it is clear
that the line integral of
which straddles the cavity and the conductor, such as the one
shown in Fig. 41. In the presence of field-lines, it is clear
that the line integral of 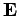 along that portion of the loop
which lies inside the cavity is non-zero. However, the line integral
of
along that portion of the loop
which lies inside the cavity is non-zero. However, the line integral
of 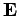 along that portion of the loop which runs through the conducting material
is obviously
zero (since
along that portion of the loop which runs through the conducting material
is obviously
zero (since
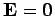 inside a conductor). Thus, the line integral of
the field around the closed loop
inside a conductor). Thus, the line integral of
the field around the closed loop  is non-zero. This, clearly contradicts
Eq. (621).
In fact, this equation implies that the line integral of the electric field
along any path which runs through the cavity, from one point on the interior surface
of the conductor to another, is zero. This can only be the case if the electric
field itself is zero everywhere inside the cavity.
There is one proviso to this argument. The electric field inside a cavity is
only zero if the cavity contains no charges. If the cavity contains charges then
our argument fails because it is possible to envisage that the line integral
of the electric field along many different paths across the cavity could be zero
without the fields along these paths necessarily being zero (this argument is
somewhat inexact: we shall improve it later on).
is non-zero. This, clearly contradicts
Eq. (621).
In fact, this equation implies that the line integral of the electric field
along any path which runs through the cavity, from one point on the interior surface
of the conductor to another, is zero. This can only be the case if the electric
field itself is zero everywhere inside the cavity.
There is one proviso to this argument. The electric field inside a cavity is
only zero if the cavity contains no charges. If the cavity contains charges then
our argument fails because it is possible to envisage that the line integral
of the electric field along many different paths across the cavity could be zero
without the fields along these paths necessarily being zero (this argument is
somewhat inexact: we shall improve it later on).
We have shown that if a cavity is completely enclosed by a conductor then no
stationary distribution of charges outside can ever produce any fields inside.
So, we can shield a piece of electrical equipment from stray external electric fields
by placing it inside a metal can.
Using similar arguments to those given above, we can also
show that no static distribution of charges inside a closed conductor can ever
produce a field outside the conductor. Clearly, shielding works both ways!
Figure 42:
 |
Let us consider some small region on the surface of a conductor. Suppose that
the local surface charge density is 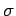 , and that the electric field just outside
the conductor is
, and that the electric field just outside
the conductor is 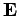 . Note that this field must be directed normal
to the surface of the conductor. Any parallel component would be shorted out
by surface currents. Another way of saying this is that the surface of a conductor
is an equipotential surface. We know that
. Note that this field must be directed normal
to the surface of the conductor. Any parallel component would be shorted out
by surface currents. Another way of saying this is that the surface of a conductor
is an equipotential surface. We know that 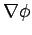 is always perpendicular to
equipotential surfaces, so
is always perpendicular to
equipotential surfaces, so
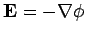 must be locally perpendicular
to a conducting surface. Let us use Gauss' law,
must be locally perpendicular
to a conducting surface. Let us use Gauss' law,
 |
(622) |
where  is a so-called Gaussian pill-box (see Fig. 42). This is a pill-box shaped volume whose two ends are aligned normal to the surface of the conductor,
with the surface running between them, and whose sides are tangential to the
surface normal.
It is clear that
is a so-called Gaussian pill-box (see Fig. 42). This is a pill-box shaped volume whose two ends are aligned normal to the surface of the conductor,
with the surface running between them, and whose sides are tangential to the
surface normal.
It is clear that 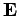 is perpendicular to the sides of the box, so the sides
make no contribution to the surface integral. The end of the box which lies
inside the conductor also makes no contribution,
since
is perpendicular to the sides of the box, so the sides
make no contribution to the surface integral. The end of the box which lies
inside the conductor also makes no contribution,
since
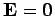 inside a conductor. Thus, the only non-zero contribution to the
surface integral comes from the end lying in free space. This contribution
is simply
inside a conductor. Thus, the only non-zero contribution to the
surface integral comes from the end lying in free space. This contribution
is simply 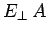 , where
, where 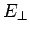 denotes an outward pointing (from the
conductor) normal
electric field, and
denotes an outward pointing (from the
conductor) normal
electric field, and 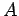 is the cross-sectional area of the box.
The charge enclosed
by the box is simply
is the cross-sectional area of the box.
The charge enclosed
by the box is simply 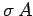 , from the definition of a surface charge density.
Thus, Gauss' law yields
, from the definition of a surface charge density.
Thus, Gauss' law yields
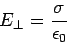 |
(623) |
as the relationship between the normal electric field immediately outside a conductor
and the surface charge density.
Figure 43:
 |
Let us look at the electric field generated by a sheet charge distribution
a little more carefully. Suppose that the charge per unit area is 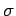 .
By symmetry, we expect the field generated below the sheet to be the mirror image
of that above the sheet (at least, locally). Thus, if we integrate Gauss' law over
a pill-box of cross sectional area
.
By symmetry, we expect the field generated below the sheet to be the mirror image
of that above the sheet (at least, locally). Thus, if we integrate Gauss' law over
a pill-box of cross sectional area 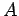 , as shown in Fig. 43, then the
two ends both contribute
, as shown in Fig. 43, then the
two ends both contribute
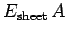 to the surface integral, where
to the surface integral, where  is the normal
electric field generated above and below the sheet. The charge enclosed
by the pill-box is just
is the normal
electric field generated above and below the sheet. The charge enclosed
by the pill-box is just 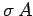 . Thus, Gauss' law yields
a symmetric electric field
. Thus, Gauss' law yields
a symmetric electric field
So, how do we get the asymmetric electric field of a conducting surface,
which is zero immediately below the surface (i.e., inside the conductor) and
non-zero immediately above it? Clearly, we have to add in an external field
(i.e., a field which is not generated locally by the sheet charge).
The
requisite field is
 |
(626) |
both above and below the charge sheet. The total field is the sum of the field
generated locally by the charge sheet and the external field. Thus, we obtain
which is in agreement with Eq. (623).
The external field exerts a force on the charge sheet. The field generated locally
by
the sheet itself obviously cannot exert a force (the sheet cannot exert
a force on itself!). The force per unit area acting on the surface of the
conductor always acts outward, and is given by
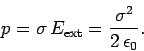 |
(629) |
Thus, there is an electrostatic pressure acting on any charged conductor.
This effect can be visualized by charging up soap bubbles: the additional
electrostatic pressure eventually causes them to burst. The electrostatic pressure
can also be written
 |
(630) |
where 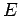 is the field strength immediately above the surface of the conductor.
Note that, according to the above formula, the electrostatic pressure is equivalent
to the energy density of the electric field immediately outside the conductor.
This is not a coincidence. Suppose that the conductor expands by an average
distance
is the field strength immediately above the surface of the conductor.
Note that, according to the above formula, the electrostatic pressure is equivalent
to the energy density of the electric field immediately outside the conductor.
This is not a coincidence. Suppose that the conductor expands by an average
distance 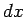 , due to the electrostatic pressure. The electric field is excluded
from the region into which the conductor expands. The volume of this region
, due to the electrostatic pressure. The electric field is excluded
from the region into which the conductor expands. The volume of this region
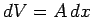 , where
, where 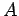 is the surface area of the conductor. Thus, the energy
of the electric field decreases by an amount
is the surface area of the conductor. Thus, the energy
of the electric field decreases by an amount
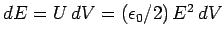 ,
where
,
where 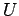 is the energy density of the field. This decrease in energy can be
ascribed to the work which the field does on the conductor in order to make it expand.
This work is
is the energy density of the field. This decrease in energy can be
ascribed to the work which the field does on the conductor in order to make it expand.
This work is 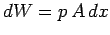 , where
, where 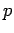 is the force per unit area the field exerts
on the conductor. Thus,
is the force per unit area the field exerts
on the conductor. Thus, 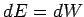 , from energy conservation, giving
, from energy conservation, giving
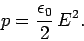 |
(631) |
This technique for calculating a force given an expression
for the energy of a
system as a function of some adjustable parameter
is called the principle of virtual work, and is very useful.
We have seen that
an electric field is excluded from the inside of the conductor, but not
from the outside, giving rise to a net outward
force. We can account for this by saying that the field exerts a
negative pressure
 on the conductor.
We know that if we evacuate a metal can then the
pressure difference between the inside and the outside eventually causes
it to implode. Likewise, if we place the can in a strong electric field then
the pressure difference between the inside and the outside will eventually cause
it to explode.
How big a field do we need before the electrostatic pressure difference
is the same as that obtained by
evacuating the can? In other words, what field exerts a negative
pressure of one atmosphere (i.e.,
on the conductor.
We know that if we evacuate a metal can then the
pressure difference between the inside and the outside eventually causes
it to implode. Likewise, if we place the can in a strong electric field then
the pressure difference between the inside and the outside will eventually cause
it to explode.
How big a field do we need before the electrostatic pressure difference
is the same as that obtained by
evacuating the can? In other words, what field exerts a negative
pressure of one atmosphere (i.e., 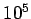 newtons per meter squared) on conductors?
The answer is a field of strength
newtons per meter squared) on conductors?
The answer is a field of strength 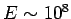 volts per meter.
Fortunately, this is a rather
large field, so there is no danger of your car exploding when you turn on the
stereo!
volts per meter.
Fortunately, this is a rather
large field, so there is no danger of your car exploding when you turn on the
stereo!



Next: Boundary conditions on the
Up: Electrostatics
Previous: Ohm's law
Richard Fitzpatrick
2006-02-02

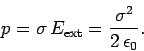
![]() on the conductor.
We know that if we evacuate a metal can then the
pressure difference between the inside and the outside eventually causes
it to implode. Likewise, if we place the can in a strong electric field then
the pressure difference between the inside and the outside will eventually cause
it to explode.
How big a field do we need before the electrostatic pressure difference
is the same as that obtained by
evacuating the can? In other words, what field exerts a negative
pressure of one atmosphere (i.e.,
on the conductor.
We know that if we evacuate a metal can then the
pressure difference between the inside and the outside eventually causes
it to implode. Likewise, if we place the can in a strong electric field then
the pressure difference between the inside and the outside will eventually cause
it to explode.
How big a field do we need before the electrostatic pressure difference
is the same as that obtained by
evacuating the can? In other words, what field exerts a negative
pressure of one atmosphere (i.e., ![]() newtons per meter squared) on conductors?
The answer is a field of strength
newtons per meter squared) on conductors?
The answer is a field of strength ![]() volts per meter.
Fortunately, this is a rather
large field, so there is no danger of your car exploding when you turn on the
stereo!
volts per meter.
Fortunately, this is a rather
large field, so there is no danger of your car exploding when you turn on the
stereo!