


Next: Conductors
Up: Electrostatics
Previous: Electrostatic energy
Ohm's law
We all know the simplest version of Ohm's law:
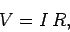 |
(609) |
where  is the voltage drop across a resistor of resistance
is the voltage drop across a resistor of resistance  when a current
when a current 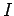 flows through it. Let us generalize this law so that it is expressed in terms
of
flows through it. Let us generalize this law so that it is expressed in terms
of 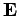 and
and 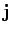 , rather than
, rather than  and
and 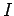 . Consider a length
. Consider a length
 of a conductor of uniform cross-sectional area
of a conductor of uniform cross-sectional area 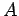 with a current
with a current
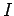 flowing down it. In general, we expect the electrical
resistance of the conductor to be proportional to its length, and inversely
proportional to its area (i.e., it is harder to push an electrical
current down a long
rather than a short wire, and it is easier to push a current down a wide rather
than a narrow conducting channel.) Thus, we can write
flowing down it. In general, we expect the electrical
resistance of the conductor to be proportional to its length, and inversely
proportional to its area (i.e., it is harder to push an electrical
current down a long
rather than a short wire, and it is easier to push a current down a wide rather
than a narrow conducting channel.) Thus, we can write
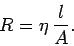 |
(610) |
The constant 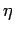 is called the resistivity, and is measured in
units of ohm-meters. Ohm's law becomes
is called the resistivity, and is measured in
units of ohm-meters. Ohm's law becomes
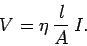 |
(611) |
However, 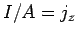 (supposing that the conductor is aligned along the
(supposing that the conductor is aligned along the  -axis)
and
-axis)
and  , so the above equation reduces to
, so the above equation reduces to
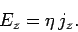 |
(612) |
There is nothing special about the  -axis (in an isotropic conducting medium), so the
previous formula immediately generalizes to
-axis (in an isotropic conducting medium), so the
previous formula immediately generalizes to
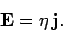 |
(613) |
This is the vector form of Ohm's law.
A charge 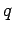 which moves through a voltage drop
which moves through a voltage drop  acquires an energy
acquires an energy 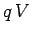 from the
electric field. In a resistor, this energy is dissipated as heat. This type of heating
is called ohmic heating. Suppose that
from the
electric field. In a resistor, this energy is dissipated as heat. This type of heating
is called ohmic heating. Suppose that 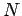 charges per unit time pass through a
resistor. The current flowing is obviously
charges per unit time pass through a
resistor. The current flowing is obviously 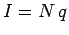 . The total energy gained by the
charges, which appears as heat inside the resistor, is
. The total energy gained by the
charges, which appears as heat inside the resistor, is
 |
(614) |
per unit time. Thus, the heating power is
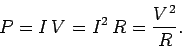 |
(615) |
Equations (614) and (615) generalize to
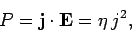 |
(616) |
where  is now the power dissipated per unit volume in a resistive medium.
is now the power dissipated per unit volume in a resistive medium.



Next: Conductors
Up: Electrostatics
Previous: Electrostatic energy
Richard Fitzpatrick
2006-02-02
![]() which moves through a voltage drop
which moves through a voltage drop ![]() acquires an energy
acquires an energy ![]() from the
electric field. In a resistor, this energy is dissipated as heat. This type of heating
is called ohmic heating. Suppose that
from the
electric field. In a resistor, this energy is dissipated as heat. This type of heating
is called ohmic heating. Suppose that ![]() charges per unit time pass through a
resistor. The current flowing is obviously
charges per unit time pass through a
resistor. The current flowing is obviously ![]() . The total energy gained by the
charges, which appears as heat inside the resistor, is
. The total energy gained by the
charges, which appears as heat inside the resistor, is