


Next: Capacitors
Up: Electrostatics
Previous: Conductors
Figure 44:
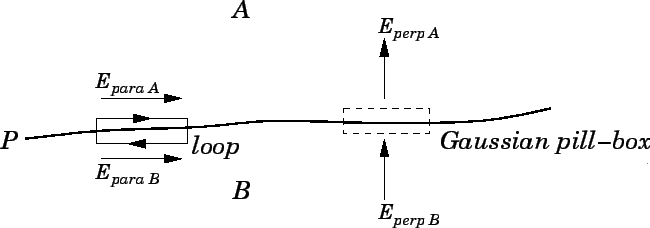 |
What are the most general boundary conditions satisfied by the electric field
at the interface between two media: e.g., the interface between a vacuum
and a conductor? Consider an interface  between two media
between two media 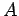 and
and 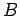 .
Let us, first of all, apply Gauss' law,
.
Let us, first of all, apply Gauss' law,
 |
(632) |
to a Gaussian pill-box  of cross-sectional area
of cross-sectional area  whose two ends are
locally parallel to the interface (see Fig. 44). The ends of the box can be made arbitrarily
close together. In this limit, the flux of the electric field out of the sides
of the box is obviously negligible. The only contribution to the flux comes
from the two ends. In fact,
whose two ends are
locally parallel to the interface (see Fig. 44). The ends of the box can be made arbitrarily
close together. In this limit, the flux of the electric field out of the sides
of the box is obviously negligible. The only contribution to the flux comes
from the two ends. In fact,
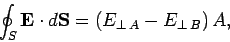 |
(633) |
where  is the perpendicular (to the interface)
electric field in
medium
is the perpendicular (to the interface)
electric field in
medium 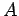 at the interface, etc. The charge enclosed by the pill-box is
simply
at the interface, etc. The charge enclosed by the pill-box is
simply 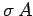 , where
, where 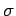 is the sheet charge density on the interface.
Note that any volume distribution of charge gives rise to a negligible contribution
to the right-hand side of the above equation, in the limit where the two
ends of the pill-box are very closely spaced. Thus, Gauss' law
yields
is the sheet charge density on the interface.
Note that any volume distribution of charge gives rise to a negligible contribution
to the right-hand side of the above equation, in the limit where the two
ends of the pill-box are very closely spaced. Thus, Gauss' law
yields
 |
(634) |
at the interface: i.e.,
the presence of a charge sheet on an interface causes a discontinuity in the
perpendicular component of the electric field. What about the parallel electric
field? Let us apply Faraday's law to a rectangular
loop  whose long sides, length
whose long sides, length  , run parallel to the interface,
, run parallel to the interface,
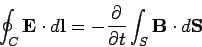 |
(635) |
(see Fig. 44).
The length of the short sides is assumed to be arbitrarily small. The dominant
contribution to the loop integral comes from the long sides:
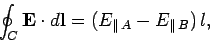 |
(636) |
where
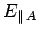 is the parallel (to the interface) electric field in
medium
is the parallel (to the interface) electric field in
medium 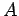 at the interface, etc. The flux of the magnetic field through the
loop is approximately
at the interface, etc. The flux of the magnetic field through the
loop is approximately 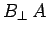 , where
, where 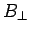 is the component of the
magnetic field which is normal to the loop, and
is the component of the
magnetic field which is normal to the loop, and 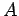 is the area of the loop.
But,
is the area of the loop.
But,
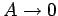 as the short sides of the loop are shrunk to zero. So,
unless the magnetic field becomes infinite (we shall assume that it does not), the
flux also tends to zero. Thus,
as the short sides of the loop are shrunk to zero. So,
unless the magnetic field becomes infinite (we shall assume that it does not), the
flux also tends to zero. Thus,
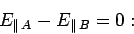 |
(637) |
i.e., there can be no discontinuity in the parallel
component of the electric field across an interface.



Next: Capacitors
Up: Electrostatics
Previous: Conductors
Richard Fitzpatrick
2006-02-02
