


Next: Rotational Hydrostatics
Up: Hydrostatics
Previous: Energy of a Floating
Figure 2.2:
Curve of buoyancy for a floating body.
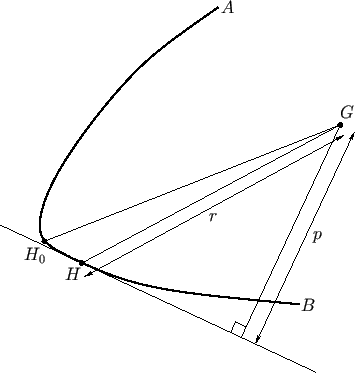 |
Consider a floating body in vertical force balance that is slowly rotated about a horizontal axis normal to one of its vertical symmetry planes.
Let us take the center of gravity, 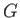 , which necessarily lies in this plane, as the origin of a coordinate system that is fixed with respect to the body.
As illustrated in Figure 2.2, as the body rotates, the locus of its center of buoyancy,
, which necessarily lies in this plane, as the origin of a coordinate system that is fixed with respect to the body.
As illustrated in Figure 2.2, as the body rotates, the locus of its center of buoyancy,  , as seen in the fixed reference frame, appears to traces out a curve,
, as seen in the fixed reference frame, appears to traces out a curve,  ,
in the plane of symmetry.
This curve is known as the curve of buoyancy. Let
,
in the plane of symmetry.
This curve is known as the curve of buoyancy. Let  represent the radial distance from the origin,
represent the radial distance from the origin, 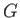 ,
to some point,
,
to some point, 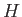 , on the curve of buoyancy. Note that the tangent to the curve of buoyancy is always orientated
horizontally. This follows because, as was shown in the previous section, small rotations of a floating body in vertical force balance
cause its center of buoyancy to shift horizontally, rather than vertically, in the plane perpendicular to the axis of rotation.
Thus, the difference in vertical height,
, on the curve of buoyancy. Note that the tangent to the curve of buoyancy is always orientated
horizontally. This follows because, as was shown in the previous section, small rotations of a floating body in vertical force balance
cause its center of buoyancy to shift horizontally, rather than vertically, in the plane perpendicular to the axis of rotation.
Thus, the difference in vertical height,  , between the center of
gravity and the center of buoyancy is equal to the perpendicular distance,
, between the center of
gravity and the center of buoyancy is equal to the perpendicular distance,  , between
, between 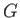 and the tangent
to the curve of buoyancy at
and the tangent
to the curve of buoyancy at 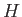 . An equilibrium configuration therefore corresponds to a maximum or a minimum of
. An equilibrium configuration therefore corresponds to a maximum or a minimum of  as
point
as
point 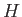 moves along the curve of buoyancy. However, the equilibrium is only stable if
moves along the curve of buoyancy. However, the equilibrium is only stable if  is minimized. If
is minimized. If 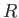 is the radius of curvature of the
curve of buoyancy then, according to a standard result in differential calculus (Lamb 1928),
is the radius of curvature of the
curve of buoyancy then, according to a standard result in differential calculus (Lamb 1928),
 |
(2.50) |
Writing this result in the form
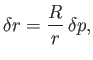 |
(2.51) |
it can be seen that maxima and minima of 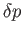 , which are the points on the
curve of buoyancy where
, which are the points on the
curve of buoyancy where
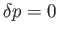 , correspond to the points where
, correspond to the points where
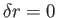 , and are,
thus, coincident with maxima and minima of
, and are,
thus, coincident with maxima and minima of  . In other words, an equilibrium configuration corresponds to
a point of maximum or minimum
. In other words, an equilibrium configuration corresponds to
a point of maximum or minimum  on the curve of buoyancy: that is, a point at which
on the curve of buoyancy: that is, a point at which 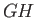 meets the
curve at right-angles. At such a point,
meets the
curve at right-angles. At such a point, 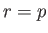 , and the potential energy consequently takes the value
, and the potential energy consequently takes the value 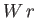 .
.
Let  be a point on the curve of buoyancy,
and let
be a point on the curve of buoyancy,
and let 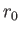 ,
, 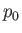 , and
, and  be the corresponding values of
be the corresponding values of  ,
,  , and
, and 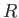 . For neighboring points on the curve, we can write
. For neighboring points on the curve, we can write
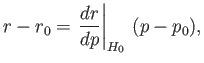 |
(2.52) |
or
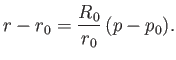 |
(2.53) |
It follows that 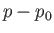 has the same sign as
has the same sign as  (because
(because  and
and 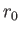 are both positive). [The fact that
are both positive). [The fact that  is positive
(i.e.,
is positive
(i.e., 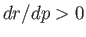 )
follows from the previously established result that the metacenter, which is the center of curvature of the curve of buoyancy, always lies above the center of buoyancy, implying
that the curve of
buoyancy is necessarily concave upwards.]
Hence,
the minima and maxima of
)
follows from the previously established result that the metacenter, which is the center of curvature of the curve of buoyancy, always lies above the center of buoyancy, implying
that the curve of
buoyancy is necessarily concave upwards.]
Hence,
the minima and maxima of  occur simultaneously with those of
occur simultaneously with those of  . Consequently, a stable equilibrium
configuration corresponds to a point of minimum
. Consequently, a stable equilibrium
configuration corresponds to a point of minimum  on the curve of buoyancy:
that is, a minimum in the distance
on the curve of buoyancy:
that is, a minimum in the distance 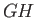 between the center of gravity and the center of buoyancy.
between the center of gravity and the center of buoyancy.
We can use the previous result to determine the stable equilibrium configurations for a beam of
square cross-section, and uniform specific gravity 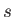 , that floats with its length horizontal.
In order to achieve this goal, we must calculate the distance
, that floats with its length horizontal.
In order to achieve this goal, we must calculate the distance 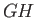 for all possible configurations
of the beam that are in vertical force balance. However, we need only consider cases where
for all possible configurations
of the beam that are in vertical force balance. However, we need only consider cases where 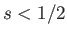 , because, according to
the analysis of Section 2.6, for every stable equilibrium configuration with
, because, according to
the analysis of Section 2.6, for every stable equilibrium configuration with 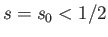 there is a corresponding stable inverted configuration with
there is a corresponding stable inverted configuration with
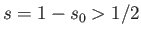 , and vice versa.
, and vice versa.
Figure 2.3:
Beam of square cross-section floating with two corners immersed.
 |
Let us define fixed rectangular axes,  and
and  , passing through the center of the middle section of the beam, and running parallel
to its sides. Let us start with the case where the waterline
, passing through the center of the middle section of the beam, and running parallel
to its sides. Let us start with the case where the waterline  is parallel to a side. (See Figure 2.3.)
If the length of a side is
is parallel to a side. (See Figure 2.3.)
If the length of a side is 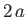 then Equation (2.16)
yields
then Equation (2.16)
yields
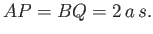 |
(2.54) |
Suppose that the beam is turned through an angle  such that the waterline assumes the position
such that the waterline assumes the position  in Figure 2.3,
but still intersects two opposite sides. The lengths
in Figure 2.3,
but still intersects two opposite sides. The lengths  and
and 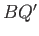 satisfy
satisfy
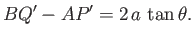 |
(2.55) |
Moreover, the area of the trapezium 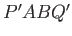 must match that of the rectangle
must match that of the rectangle  in order to ensure that the submerged volume remains invariant (otherwise, the beam would not remain in vertical force balance): that is,
in order to ensure that the submerged volume remains invariant (otherwise, the beam would not remain in vertical force balance): that is,
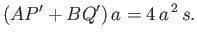 |
(2.56) |
It follows that
The constraint that the waterline intersect two opposite sides of the beam implies that  , and, hence, that
, and, hence, that
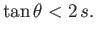 |
(2.59) |
The coordinates of the center of buoyancy, 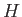 , which is the mean center of the trapezium
, which is the mean center of the trapezium 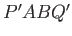 , are
, are
where
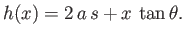 |
(2.62) |
Thus, if
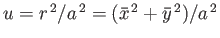 then
then
![$\displaystyle u = \frac{t^{\,2}}{36\,s^{\,2}} + \left[(1-s)-\frac{t^{\,2}}{12\,s}\right]^{\,2},$](img753.png) |
(2.63) |
where
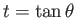 . A stable equilibrium state corresponds to a minimum of
. A stable equilibrium state corresponds to a minimum of  with respect to
with respect to  , and, hence, of
, and, hence, of 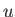 with respect to
with respect to 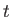 .
However,
.
However,
The minima and maxima of 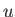 occur when
occur when 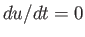 ,
,
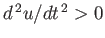 and
and 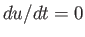 ,
,
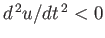 , respectively.
It follows that the symmetrical position,
, respectively.
It follows that the symmetrical position,  , in which the sides of the beam are either parallel or perpendicular to the
waterline, is always an equilibrium, but is only stable when
, in which the sides of the beam are either parallel or perpendicular to the
waterline, is always an equilibrium, but is only stable when
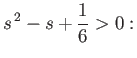 |
(2.66) |
that is, when
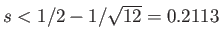 .
It is also possible to obtain equilibria in asymmetric positions such that
.
It is also possible to obtain equilibria in asymmetric positions such that 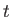 is the root of
is the root of
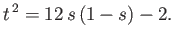 |
(2.67) |
Such equilibria only exist for 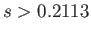 , and are stable. Finally, in order to satisfy the constraint (2.59), we
must have
, and are stable. Finally, in order to satisfy the constraint (2.59), we
must have 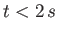 , which, in combination with the previous equation, implies that
, which, in combination with the previous equation, implies that
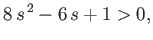 |
(2.68) |
or 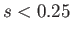 .
.
Figure 2.4:
Beam of square cross-section floating with one corner immersed.
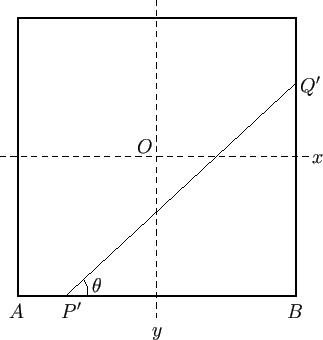 |
Suppose that the constraint (2.59) is not satisfied, so that the immersed portion of the beam's cross-section
is triangular. (See Figure 2.4.) It is clear that
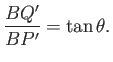 |
(2.69) |
Moreover, the area of the triangle 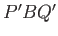 in Figure 2.4 must match that of the rectangle
in Figure 2.4 must match that of the rectangle  in
Figure 2.3, in order to ensure that the submerged volume remain invariant: that is,
in
Figure 2.3, in order to ensure that the submerged volume remain invariant: that is,
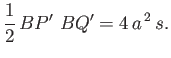 |
(2.70) |
It follows that
or, writing
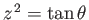 and
and
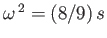 ,
,
The coordinates of the center of buoyancy, 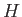 , which is the mean center of triangle
, which is the mean center of triangle 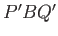 , are
, are
because the perpendicular distance of the mean center of a triangle from one of its sides is one third of the perpendicular distance
from the side to the opposite vertex.
Thus, if
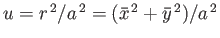 then
then
Moreover, the constraint (2.59) yields
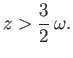 |
(2.80) |
The stable and unstable equilibria correspond to 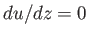 ,
,
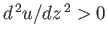 and
and 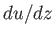 ,
,
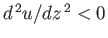 , respectively.
It follows that the symmetrical position,
, respectively.
It follows that the symmetrical position,  , in which the diagonals of the beam are either parallel or perpendicular to the
waterline is an equilibrium provided
, in which the diagonals of the beam are either parallel or perpendicular to the
waterline is an equilibrium provided
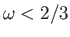 , or
, or 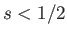 , but is only stable when
, but is only stable when
 , or
, or
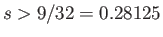 .
It is also possible to obtain equilibria in asymmetric positions such that
.
It is also possible to obtain equilibria in asymmetric positions such that  is the root of
is the root of
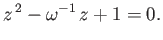 |
(2.81) |
Such equilibria only exist for
 , or
, or
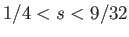 , and are stable.
, and are stable.
In summary, the stable equilibrium configurations of a beam of square cross-section, floating with its length horizontal, are such that
the sides are either parallel or perpendicular to the waterline for  , such
that two corners are immersed but the sides and diagonals are neither parallel nor perpendicular to the waterline for
, such
that two corners are immersed but the sides and diagonals are neither parallel nor perpendicular to the waterline for
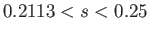 , such that only one corner is immersed but the
sides and diagonals are neither parallel nor perpendicular to the waterline for
, such that only one corner is immersed but the
sides and diagonals are neither parallel nor perpendicular to the waterline for
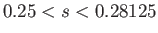 , and such that the diagonals are either parallel or perpendicular to waterline for
, and such that the diagonals are either parallel or perpendicular to waterline for
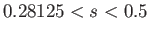 . For
. For 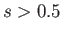 , the stable configurations are the same as those for a
beam with the complimentary specific gravity
, the stable configurations are the same as those for a
beam with the complimentary specific gravity 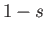 .
.



Next: Rotational Hydrostatics
Up: Hydrostatics
Previous: Energy of a Floating
Richard Fitzpatrick
2016-03-31

![]() , which necessarily lies in this plane, as the origin of a coordinate system that is fixed with respect to the body.
As illustrated in Figure 2.2, as the body rotates, the locus of its center of buoyancy,
, which necessarily lies in this plane, as the origin of a coordinate system that is fixed with respect to the body.
As illustrated in Figure 2.2, as the body rotates, the locus of its center of buoyancy, ![]() , as seen in the fixed reference frame, appears to traces out a curve,
, as seen in the fixed reference frame, appears to traces out a curve, ![]() ,
in the plane of symmetry.
This curve is known as the curve of buoyancy. Let
,
in the plane of symmetry.
This curve is known as the curve of buoyancy. Let ![]() represent the radial distance from the origin,
represent the radial distance from the origin, ![]() ,
to some point,
,
to some point, ![]() , on the curve of buoyancy. Note that the tangent to the curve of buoyancy is always orientated
horizontally. This follows because, as was shown in the previous section, small rotations of a floating body in vertical force balance
cause its center of buoyancy to shift horizontally, rather than vertically, in the plane perpendicular to the axis of rotation.
Thus, the difference in vertical height,
, on the curve of buoyancy. Note that the tangent to the curve of buoyancy is always orientated
horizontally. This follows because, as was shown in the previous section, small rotations of a floating body in vertical force balance
cause its center of buoyancy to shift horizontally, rather than vertically, in the plane perpendicular to the axis of rotation.
Thus, the difference in vertical height, ![]() , between the center of
gravity and the center of buoyancy is equal to the perpendicular distance,
, between the center of
gravity and the center of buoyancy is equal to the perpendicular distance, ![]() , between
, between ![]() and the tangent
to the curve of buoyancy at
and the tangent
to the curve of buoyancy at ![]() . An equilibrium configuration therefore corresponds to a maximum or a minimum of
. An equilibrium configuration therefore corresponds to a maximum or a minimum of ![]() as
point
as
point ![]() moves along the curve of buoyancy. However, the equilibrium is only stable if
moves along the curve of buoyancy. However, the equilibrium is only stable if ![]() is minimized. If
is minimized. If ![]() is the radius of curvature of the
curve of buoyancy then, according to a standard result in differential calculus (Lamb 1928),
is the radius of curvature of the
curve of buoyancy then, according to a standard result in differential calculus (Lamb 1928),

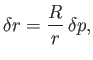
![]() be a point on the curve of buoyancy,
and let
be a point on the curve of buoyancy,
and let ![]() ,
, ![]() , and
, and ![]() be the corresponding values of
be the corresponding values of ![]() ,
, ![]() , and
, and ![]() . For neighboring points on the curve, we can write
. For neighboring points on the curve, we can write
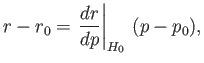
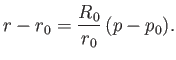
![]() , that floats with its length horizontal.
In order to achieve this goal, we must calculate the distance
, that floats with its length horizontal.
In order to achieve this goal, we must calculate the distance ![]() for all possible configurations
of the beam that are in vertical force balance. However, we need only consider cases where
for all possible configurations
of the beam that are in vertical force balance. However, we need only consider cases where ![]() , because, according to
the analysis of Section 2.6, for every stable equilibrium configuration with
, because, according to
the analysis of Section 2.6, for every stable equilibrium configuration with ![]() there is a corresponding stable inverted configuration with
there is a corresponding stable inverted configuration with
![]() , and vice versa.
, and vice versa.
![]() and
and ![]() , passing through the center of the middle section of the beam, and running parallel
to its sides. Let us start with the case where the waterline
, passing through the center of the middle section of the beam, and running parallel
to its sides. Let us start with the case where the waterline ![]() is parallel to a side. (See Figure 2.3.)
If the length of a side is
is parallel to a side. (See Figure 2.3.)
If the length of a side is ![]() then Equation (2.16)
yields
then Equation (2.16)
yields
![]() such that the waterline assumes the position
such that the waterline assumes the position ![]() in Figure 2.3,
but still intersects two opposite sides. The lengths
in Figure 2.3,
but still intersects two opposite sides. The lengths ![]() and
and ![]() satisfy
satisfy
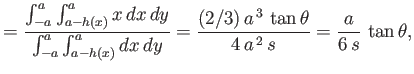
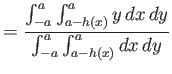

![$\displaystyle u = \frac{t^{\,2}}{36\,s^{\,2}} + \left[(1-s)-\frac{t^{\,2}}{12\,s}\right]^{\,2},$](img753.png)
![$\displaystyle = \frac{t}{36\,s^{\,2}}\left[t^{\,2}-12\,s\,(1-s)+2\right],$](img757.png)
![$\displaystyle = \frac{1}{36\,s^{\,2}}\left[3\,t^{\,2}-12\,s\,(1-s)+2\right].$](img759.png)
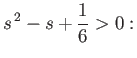
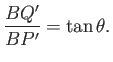
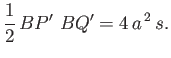

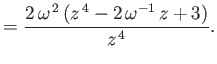
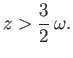
![]() , such
that two corners are immersed but the sides and diagonals are neither parallel nor perpendicular to the waterline for
, such
that two corners are immersed but the sides and diagonals are neither parallel nor perpendicular to the waterline for
![]() , such that only one corner is immersed but the
sides and diagonals are neither parallel nor perpendicular to the waterline for
, such that only one corner is immersed but the
sides and diagonals are neither parallel nor perpendicular to the waterline for
![]() , and such that the diagonals are either parallel or perpendicular to waterline for
, and such that the diagonals are either parallel or perpendicular to waterline for
![]() . For
. For ![]() , the stable configurations are the same as those for a
beam with the complimentary specific gravity
, the stable configurations are the same as those for a
beam with the complimentary specific gravity ![]() .
.