Next: Vertical Stability of Floating
Up: Hydrostatics
Previous: Buoyancy
Equilibrium of Floating Bodies
Consider the situation described in the previous section.
Suppose that the fluid contained within  is replaced by a partially submerged solid body whose outer surface
corresponds to
is replaced by a partially submerged solid body whose outer surface
corresponds to  . Furthermore, suppose that this body is in mechanical equilibrium with the surrounding fluid (i.e., it is stationary, and floating on the surface of the water).
It follows that the pressure distribution in the surrounding fluid is unchanged [because the force balance criterion (2.3) can be integrated to give the pressure distribution (2.4) at all contiguous points in the fluid, provided that the fluid remains
in mechanical equilibrium].
We conclude that the net surface force acting across
. Furthermore, suppose that this body is in mechanical equilibrium with the surrounding fluid (i.e., it is stationary, and floating on the surface of the water).
It follows that the pressure distribution in the surrounding fluid is unchanged [because the force balance criterion (2.3) can be integrated to give the pressure distribution (2.4) at all contiguous points in the fluid, provided that the fluid remains
in mechanical equilibrium].
We conclude that the net surface force acting across  is also unchanged (because this is directly related to the
pressure distribution in the fluid immediately surrounding
is also unchanged (because this is directly related to the
pressure distribution in the fluid immediately surrounding  ), which implies that the
buoyancy force acting on the
floating body is the same as that acting on the displaced water: that is, the water that previously
occupied
), which implies that the
buoyancy force acting on the
floating body is the same as that acting on the displaced water: that is, the water that previously
occupied  .
In other words, from Equation (2.12),
.
In other words, from Equation (2.12),
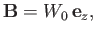 |
(2.14) |
where
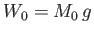 and
and  are the weight and mass of the displaced water, respectively. The fact that the
buoyancy force is unchanged also implies that the vertical line of action of
are the weight and mass of the displaced water, respectively. The fact that the
buoyancy force is unchanged also implies that the vertical line of action of 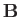 passes through the center of gravity,
passes through the center of gravity, 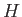 (say), of the displaced water. Incidentally,
(say), of the displaced water. Incidentally, 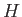 is generally
known as the center of buoyancy.
is generally
known as the center of buoyancy.
A floating body of weight 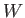 is acted upon by two forces: namely, its own weight,
is acted upon by two forces: namely, its own weight,
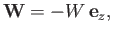 |
(2.15) |
and the buoyancy force,
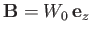 , due to the pressure of the surrounding water.
Of course, the line of action of
, due to the pressure of the surrounding water.
Of course, the line of action of 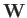 passes through the body's center of gravity,
passes through the body's center of gravity, 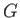 (say).
So as to remain in equilibrium, the body must be subject to zero net force and zero net torque.
The requirement of zero net force yields
(say).
So as to remain in equilibrium, the body must be subject to zero net force and zero net torque.
The requirement of zero net force yields  . In other words, in equilibrium, the weight of the water displaced by a floating body
is equal to the weight of the body, or, alternatively, in equilibrium, the magnitude of the buoyancy force acting on a floating body is equal to the weight of the
displaced water. This famous result is known as Archimedes' principle, after Archimedes of Syracuse (c. 278-212 BCE). The requirement of
zero net torque implies that, in equilibrium, the center of gravity,
. In other words, in equilibrium, the weight of the water displaced by a floating body
is equal to the weight of the body, or, alternatively, in equilibrium, the magnitude of the buoyancy force acting on a floating body is equal to the weight of the
displaced water. This famous result is known as Archimedes' principle, after Archimedes of Syracuse (c. 278-212 BCE). The requirement of
zero net torque implies that, in equilibrium, the center of gravity, 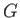 , and center of buoyancy,
, and center of buoyancy, 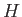 , of
a floating body must lie on the same vertical straight-line.
, of
a floating body must lie on the same vertical straight-line.
Consider a floating body of mass 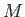 and volume
and volume  .
Let
.
Let
 be the body's
mean mass density. Archimedes' principle implies that, in equilibrium,
be the body's
mean mass density. Archimedes' principle implies that, in equilibrium,
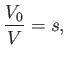 |
(2.16) |
where
 |
(2.17) |
is termed the body's specific gravity. (Recall, that 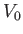 is the submerged volume, and
is the submerged volume, and 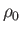 the
mass density of water.)
We conclude, from Equation (2.16), that the volume fraction of a floating body that is submerged is equal to the body's
specific gravity. Obviously, the specific gravity must be less than unity, because the
submerged volume fraction cannot exceed unity.
In fact, if the specific gravity exceeds unity then it is impossible for the buoyancy force to balance the body's weight, and the body
consequently sinks.
the
mass density of water.)
We conclude, from Equation (2.16), that the volume fraction of a floating body that is submerged is equal to the body's
specific gravity. Obviously, the specific gravity must be less than unity, because the
submerged volume fraction cannot exceed unity.
In fact, if the specific gravity exceeds unity then it is impossible for the buoyancy force to balance the body's weight, and the body
consequently sinks.
Consider a body of volume  and specific gravity
and specific gravity 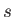 that floats in equilibrium. It follows, from Equation (2.16),
that the submerged volume is
that floats in equilibrium. It follows, from Equation (2.16),
that the submerged volume is 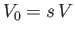 . Hence, the volume above the waterline is
. Hence, the volume above the waterline is
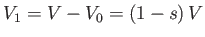 .
Suppose that the body is inverted such that its previously submerged part is raised above the waterline, and vice versa: that is,
.
Suppose that the body is inverted such that its previously submerged part is raised above the waterline, and vice versa: that is,
 . According to Equation (2.16), the body can only remain in equilibrium in this configuration if its specific gravity is
. According to Equation (2.16), the body can only remain in equilibrium in this configuration if its specific gravity is
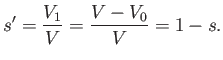 |
(2.18) |
We conclude that for every equilibrium configuration of a floating body of specific gravity 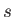 there exists
an inverted equilibrium configuration for a body of the same shape having the complementary
specific gravity
there exists
an inverted equilibrium configuration for a body of the same shape having the complementary
specific gravity 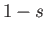 .
.



Next: Vertical Stability of Floating
Up: Hydrostatics
Previous: Buoyancy
Richard Fitzpatrick
2016-03-31
![]() is acted upon by two forces: namely, its own weight,
is acted upon by two forces: namely, its own weight,
![]() and volume
and volume ![]() .
Let
.
Let
![]() be the body's
mean mass density. Archimedes' principle implies that, in equilibrium,
be the body's
mean mass density. Archimedes' principle implies that, in equilibrium,

![]() and specific gravity
and specific gravity ![]() that floats in equilibrium. It follows, from Equation (2.16),
that the submerged volume is
that floats in equilibrium. It follows, from Equation (2.16),
that the submerged volume is ![]() . Hence, the volume above the waterline is
. Hence, the volume above the waterline is
![]() .
Suppose that the body is inverted such that its previously submerged part is raised above the waterline, and vice versa: that is,
.
Suppose that the body is inverted such that its previously submerged part is raised above the waterline, and vice versa: that is,
![]() . According to Equation (2.16), the body can only remain in equilibrium in this configuration if its specific gravity is
. According to Equation (2.16), the body can only remain in equilibrium in this configuration if its specific gravity is