


Next: Equilibrium of a Rotating
Up: Hydrostatics
Previous: Curve of Buoyancy
Consider the equilibrium of an incompressible fluid that is uniformly rotating at a
fixed angular velocity
 in some inertial frame of reference. Of course, such a fluid appears stationary in a non-inertial co-rotating reference frame. Moreover, according to standard Newtonian dynamics (Fitzpatrick 2012), the force balance equation for the fluid in the
co-rotating frame takes the form (cf., Section 2.2)
in some inertial frame of reference. Of course, such a fluid appears stationary in a non-inertial co-rotating reference frame. Moreover, according to standard Newtonian dynamics (Fitzpatrick 2012), the force balance equation for the fluid in the
co-rotating frame takes the form (cf., Section 2.2)
where  is the static fluid pressure,
is the static fluid pressure,  the mass density,
the mass density,
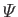 the gravitational potential energy
per unit mass, and
the gravitational potential energy
per unit mass, and  a position vector (measured with respect to an origin that lies on the
axis of rotation). The final term on the right-hand side of the previous equation represents the fictitious centrifugal force density.
Without loss of generality, we can assume that
a position vector (measured with respect to an origin that lies on the
axis of rotation). The final term on the right-hand side of the previous equation represents the fictitious centrifugal force density.
Without loss of generality, we can assume that

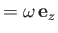 . It follows
that
. It follows
that
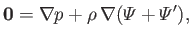 |
(2.83) |
where
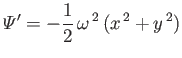 |
(2.84) |
is the so-called centrifugal potential.
Recall, incidentally, that  is a uniform constant in an incompressible fluid.
is a uniform constant in an incompressible fluid.
As an example, consider the equilibrium of a body of water, located on the Earth's surface, that is uniformly rotating about a vertical
axis at the fixed angular velocity  . It is convenient to adopt cylindrical
coordinates (see Section C.3),
. It is convenient to adopt cylindrical
coordinates (see Section C.3),  ,
,  ,
,  , whose symmetry axis coincides with the axis of rotation. Let
, whose symmetry axis coincides with the axis of rotation. Let  increase upward. It follows
that
increase upward. It follows
that
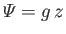 and
and
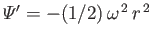 . Assuming that the pressure distribution is axisymmetric,
so that
. Assuming that the pressure distribution is axisymmetric,
so that  , the force balance equation, (2.83), reduces to
, the force balance equation, (2.83), reduces to
or
The previous two equations can be integrated to give
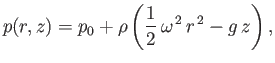 |
(2.89) |
where 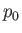 is a constant. Thus, constant pressure surfaces in a uniformly rotating
body of water take the form of paraboloids of revolution about the rotation axis. Suppose that
is a constant. Thus, constant pressure surfaces in a uniformly rotating
body of water take the form of paraboloids of revolution about the rotation axis. Suppose that 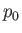 represents
atmospheric pressure. In this case, the surface of the water is the locus of
represents
atmospheric pressure. In this case, the surface of the water is the locus of
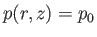 : that is,
it is the constant pressure surface whose pressure matches that of the atmosphere. It follows that the
surface of the water is the paraboloid of revolution
: that is,
it is the constant pressure surface whose pressure matches that of the atmosphere. It follows that the
surface of the water is the paraboloid of revolution
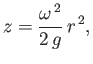 |
(2.90) |
where  is the perpendicular distance from the axis
of rotation, and
is the perpendicular distance from the axis
of rotation, and  the on-axis height of the surface.
the on-axis height of the surface.
According to the analysis of Section 2.3, the buoyancy force acting on any co-rotating solid body, which is wholly or
partially immersed in the water, is the same as that which would maintain the
mass of water displaced by the body in relative equilibrium. In the case of a floating body, this mass is
limited by the continuation of the water's curved surface through the body. Let points 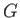 and
and
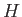 represent the centers of gravity and buoyancy, respectively, of the body. Of course, the latter point is
simply the center of gravity of the displaced water. Suppose that
represent the centers of gravity and buoyancy, respectively, of the body. Of course, the latter point is
simply the center of gravity of the displaced water. Suppose that 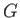 and
and 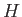 are located perpendicular
distances
are located perpendicular
distances  and
and 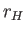 from the axis of rotation, respectively. Finally, let
from the axis of rotation, respectively. Finally, let 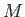 be the mass of the body, and
be the mass of the body, and
 the mass of the displaced water. It follows that the buoyancy force has an upward vertical
component
the mass of the displaced water. It follows that the buoyancy force has an upward vertical
component 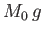 , and an outward horizontal component
, and an outward horizontal component
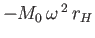 . Thus, according to
standard Newtonian dynamics (Fitzpatrick 2012), the
equation of horizontal motion of a general co-rotating body is
. Thus, according to
standard Newtonian dynamics (Fitzpatrick 2012), the
equation of horizontal motion of a general co-rotating body is
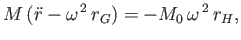 |
(2.91) |
where
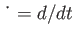 .
From Archimedes' principle,
.
From Archimedes' principle, 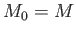 for the case of a floating body that is less dense than water.
However, if the body is of uniform density then
for the case of a floating body that is less dense than water.
However, if the body is of uniform density then 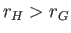 , as a consequence of the curvature of the water's surface. Hence,
we obtain
, as a consequence of the curvature of the water's surface. Hence,
we obtain
 |
(2.92) |
In other words, a floating body drifts radially inward towards the rotation axis. On the other hand, 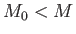 for a fully submerged
body that is more dense than water. However, if the body is of uniform density then its centers of
gravity and buoyancy coincide with one another, so that
for a fully submerged
body that is more dense than water. However, if the body is of uniform density then its centers of
gravity and buoyancy coincide with one another, so that 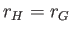 . Hence, we obtain
. Hence, we obtain
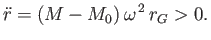 |
(2.93) |
In other words, a fully submerged body drifts radially outward from the rotation axis. The previous analysis accounts for the
common observation that objects heavier than water, such as grains of sand, tend to
collect on the outer side of a bend in a fast flowing river, while floating objects, such as sticks,
tend to collect on the inner side.



Next: Equilibrium of a Rotating
Up: Hydrostatics
Previous: Curve of Buoyancy
Richard Fitzpatrick
2016-03-31
![]() . It is convenient to adopt cylindrical
coordinates (see Section C.3),
. It is convenient to adopt cylindrical
coordinates (see Section C.3), ![]() ,
, ![]() ,
, ![]() , whose symmetry axis coincides with the axis of rotation. Let
, whose symmetry axis coincides with the axis of rotation. Let ![]() increase upward. It follows
that
increase upward. It follows
that
![]() and
and
![]() . Assuming that the pressure distribution is axisymmetric,
so that
. Assuming that the pressure distribution is axisymmetric,
so that ![]() , the force balance equation, (2.83), reduces to
, the force balance equation, (2.83), reduces to
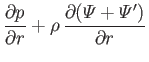
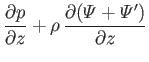
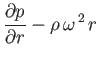
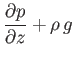
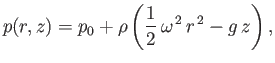
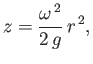
![]() and
and
![]() represent the centers of gravity and buoyancy, respectively, of the body. Of course, the latter point is
simply the center of gravity of the displaced water. Suppose that
represent the centers of gravity and buoyancy, respectively, of the body. Of course, the latter point is
simply the center of gravity of the displaced water. Suppose that ![]() and
and ![]() are located perpendicular
distances
are located perpendicular
distances ![]() and
and ![]() from the axis of rotation, respectively. Finally, let
from the axis of rotation, respectively. Finally, let ![]() be the mass of the body, and
be the mass of the body, and
![]() the mass of the displaced water. It follows that the buoyancy force has an upward vertical
component
the mass of the displaced water. It follows that the buoyancy force has an upward vertical
component ![]() , and an outward horizontal component
, and an outward horizontal component
![]() . Thus, according to
standard Newtonian dynamics (Fitzpatrick 2012), the
equation of horizontal motion of a general co-rotating body is
. Thus, according to
standard Newtonian dynamics (Fitzpatrick 2012), the
equation of horizontal motion of a general co-rotating body is